Здравствуйте найти промежутки возрастания, убывания и экстремумы функции, если можно то на листочке большое
Ответы на вопрос:
Пошаговое объяснение:
у=х⁴-4х³-8х²+12
1) Область определения функции.
D(f) = R
2) Находим производную функции.
у' = 4х³-12х²-16х
3)Найдем нули производной:
y' = 0;
4х³-12х²-16х=0
4х(х²-3х-4)=0,
х₁=0, х₂=4 , х₃=-1 - критические точки (точки экстремума)
4) Получилось четыре промежутка:
(-∞; -1), (-1;0), (0; 4) и (4; +∞).
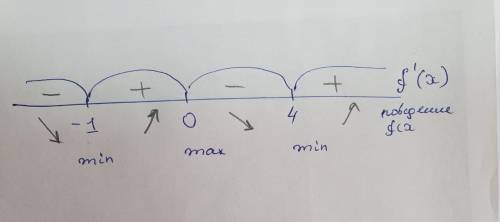
5) Расставим знаки производной на каждом промежутке:
(-∞; -1) если х = -2: y'(-2) = -8(4+6-4)= <0 (минус).
(-1;0) если х = 1: y'(-0,5) = -2(0,25+1,5-4) = 4,5 >0 (плюс).
(0; 4) если х = 1: y'(1) = 4(1-3-4) <0 (минус).
(4; +∞) если х = 5: y'(5) = 20(25-15-4) >0 (плюс).
6)Определяем промежутки возрастания и убывания функции
Если знак производной функции на промежутке положительный, то функция возрастает, если отрицательный - то убывает.
Функция возрастает (производная плюс) на х∈ (-1;0), (4;+∞)
Функция убывает на х∈ (-∞; -1) и (0;4;)
точка минимума функции х=-1; 4; точка максимума функции х=0.
f(x) max = f(0) = 12, минимум (0;12)
f(x) min =f(-1) = (-1)⁴-4*(-1)³-8*(-1)²+12 = 1+4-8+12=9
f(x) min =f(4) = (4)⁴-4*(4)³-8*(4)²+12=256-256-128+12=116
максимум (-1;9), (4; -116)
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Запиши выражение равные данным используя сочетательное свойство умножения...
 Yandarbieva106.05.2023 02:21
Yandarbieva106.05.2023 02:21 -
Всаду растут 125 деревьев: яблони вишни и сливы. яблонь и вишен 105, вишен...
 Петья05.06.2021 05:57
Петья05.06.2021 05:57 -
Найти площадь круга если диаметр 12см...
 nkaracheva03.03.2022 09:35
nkaracheva03.03.2022 09:35 -
Водном мешке было 30 килограмм гречки в другом 45 килограмм всю крышку...
 alexandrafortun11.03.2023 02:06
alexandrafortun11.03.2023 02:06 -
20% от 40% числа б равны 5,6.найти б (решите ! )...
 davlud197417.08.2021 16:05
davlud197417.08.2021 16:05 -
Запишите масштаб карты, если отрезок на местности в 1км изображается на...
 Abuhgghhhhhh19.03.2022 14:07
Abuhgghhhhhh19.03.2022 14:07 -
15 если ответ те сколько мне нет если я родилась 2005 года 16 января...
 СашаТарсюк01.04.2023 13:32
СашаТарсюк01.04.2023 13:32 -
Тема: линейное кравнение с одной переменой примеры: 6,75х=2целых1\4х-9...
 alesiakorneva29.04.2023 16:18
alesiakorneva29.04.2023 16:18 -
Решите уравнение: (4x^2- 6x + 5) + (-4x^2 - 8x) = 11....
 DarkDanilka03.10.2022 17:35
DarkDanilka03.10.2022 17:35 -
Какие 2вектора называют перпендикулярно...
 kazinka915.03.2023 11:36
kazinka915.03.2023 11:36

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
