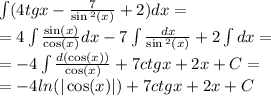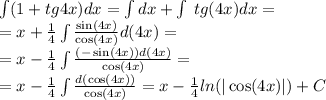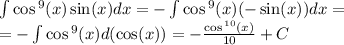Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
То представьте в виде степени и найдите значи 1) 5(5а ) а при а- (0,2); ...
 RaiderUp18.03.2021 02:34
RaiderUp18.03.2021 02:34 -
Номер 1 какое из утверждений не верно? решите его 1) n+p больше 0 2)p-n больше...
 Mika12312304.07.2020 22:22
Mika12312304.07.2020 22:22 -
Выражение. (можно фоткой) (3/9-х2 + 1/х-3) / х/х2-6х+9...
 Блиллиант281215.01.2023 12:14
Блиллиант281215.01.2023 12:14 -
Водной цистерне было 200 литров воды а в другой 640 л ,когда из 2 использовали...
 Avenrop23610.05.2020 21:57
Avenrop23610.05.2020 21:57 -
Автобусні квитки мають номери 000 000 до 999 999. квиток називають щасливим...
 balbasenok04.04.2020 13:34
balbasenok04.04.2020 13:34 -
Бросают игральный кубик. сравните шансы наступления событий a: выпадет три...
 nek44415.03.2022 03:17
nek44415.03.2022 03:17 -
Число 5 є коренем рівняння 2x²-5x+n=0. знайдіть другий корінь рівняння і значення...
 palechov0113.06.2021 11:43
palechov0113.06.2021 11:43 -
4. Решите уравнение: (2-x)^2-x(x+3/2)=4...
 BearSlesher17.06.2020 00:32
BearSlesher17.06.2020 00:32 -
Вот задание, решите не могу решить, потому что был на Карантине...
 MaksPlay220905.12.2021 02:51
MaksPlay220905.12.2021 02:51 -
При каких значениях переменной выражение by в квадрате+3y-2 имеет смысл! Умоляю...
 Diana1500710.02.2023 06:51
Diana1500710.02.2023 06:51

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

 !
!