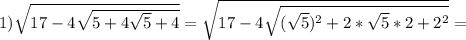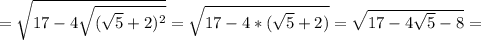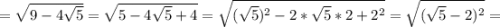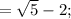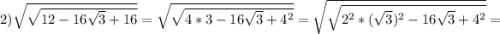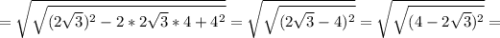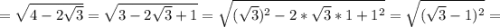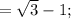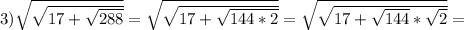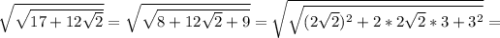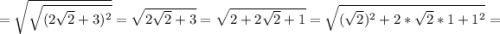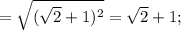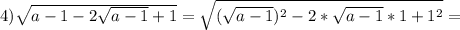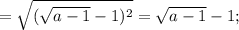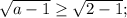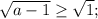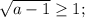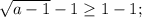Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Найти dz( с решением): а) (х+2у)у^2 б) cos(2x+e^y) найти значения частных...
 Пам90430.08.2021 19:28
Пам90430.08.2021 19:28 -
Найди область определения функции y=lg(34-|2+5x|)...
 ZloyFuzz16.09.2022 10:31
ZloyFuzz16.09.2022 10:31 -
Абрикосы при сушке теряют 60% своей массы. сколько получится сушеных абрикосов...
 Малефисента111111126.08.2020 12:00
Малефисента111111126.08.2020 12:00 -
При открытии фермы поголовье стада составляло 200 коров. через 2 года...
 ALLAHJIJA28.02.2020 02:47
ALLAHJIJA28.02.2020 02:47 -
Запишите в виде обыкновенной дроби бесконечную десятичную 0,32(45)...
 Rudisaleh22.04.2020 12:31
Rudisaleh22.04.2020 12:31 -
X^4-8x^2-9=0 розв язати рівняння дискримінант...
 MaiorPeZDoBi405.03.2021 13:34
MaiorPeZDoBi405.03.2021 13:34 -
На весенней распродаже стоимость пальто уменьшилась на 30% сколько стало...
 751557516.04.2021 09:42
751557516.04.2021 09:42 -
Велосипедист ехал 2ч по лесной дороге и 1ч по шоссе, всего он проехал...
 vladuxa031127.02.2021 01:26
vladuxa031127.02.2021 01:26 -
За 4 години човен проходить за течією річки і таку саму відстань як за...
 Gabueva0203.06.2022 00:12
Gabueva0203.06.2022 00:12 -
При каких значений параметра p уравнения x^2+px+42=0 имеет корень, равный...
 лиза267707.05.2022 00:16
лиза267707.05.2022 00:16

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.