Регистрация Спросить otvet5GPT
Даня1681
06.06.2021 21:12
Алгебра
Есть ответ 👍

с вариантом е только попонятнее ​

201
371
Посмотреть ответы 2

Ответы на вопрос:

hdblin530
hdblin530
4,8(98 оценок)

Текста много, но надеюсь я понятно всё объяснила...

Формула нахождения n-ного члена арифметической прогрессии выглядит как а n-нное = а1 + (n - 1)d.

Нам не известны ни а1, ни d, но не обращаем на это внимание, ведь нам даны значения а5 и а8. Тогда запишем в систему:

а5 = а1 + (5 - 1)d

а8 = а1 + (8 - 1)d

Получается (всё так же объединяем системой):

а5 = а1 + 4d

а8 = а1 + 7d

Подставим данные нам значения а5 и а8(всё так же системой)

-10 = а1 + 4d

8 = а1 + 7d

А теперь выполним вычитание и а1 уничтожиться:

-18 = -3d

d = 6

Дальше очень просто получить а1, подставив полученное d в уравнение а5 или а8. Я подставлю в а5

а5 = а1 + 4d

-10 = а1 + 24

а1 = -34

Теперь по формуле n-ного члена ариф.прогрессии найдём а6:

а6 = а1 + 5d

а6 = -34 + 30

а6 = -4

ответ: а1 = -34, а6 = -4

янннак
янннак
4,4(22 оценок)

\sqrt[8]{256-64\sqrt6}\left(\frac12\sqrt{\frac15(10+\sqrt{5(10+\sqrt5(8-3\sqrt6))})}+i\frac1{2\sqrt{\frac5{10-\sqrt{5(10+\sqrt{5(8-3\sqrt6)})}}}}\right)

в обычной записи

и

\sqrt[4]{-8+(4+4i)\sqrt6}

в более удобной

Объяснение:

Вычисляем по частям

\displaystyle 8\sqrt{3i}=8\sqrt3\sqrt i=8\sqrt3(\cos\frac\pi4+i\sin\frac\pi4)=4\sqrt3\sqrt2+4\sqrt3\sqrt2i\\-8+8\sqrt{3i}=-8+4\sqrt3\sqrt2+4\sqrt3\sqrt2i\\\sqrt[4]{-8+8\sqrt{3i}}=\sqrt[4]{a+bi}

При этом

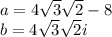
a=4\sqrt3\sqrt2-8\\b=4\sqrt3\sqrt2i

\displaystyle \sqrt[4]{a+bi}=\sqrt[8]{a^2+b^2}(\cos(\frac14\arctan(\frac{b}{a}) )+i\sin(\frac14\arctan(\frac{b}{a})))

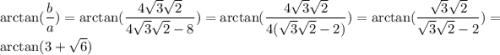
\displaystyle \arctan(\frac{b}{a})= \arctan(\frac{4\sqrt3\sqrt2}{4\sqrt3\sqrt2-8})=\arctan(\frac{4\sqrt3\sqrt2}{4(\sqrt3\sqrt2-2)})=\arctan(\frac{\sqrt3\sqrt2}{\sqrt3\sqrt2-2})=\arctan(3+\sqrt6)

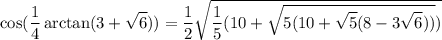
\displaystyle\cos( \frac14\arctan(3+\sqrt6))=\frac12\sqrt{\frac15(10+\sqrt{5(10+\sqrt5(8-3\sqrt6))})}

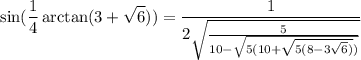
\displaystyle \sin(\frac14\arctan(3+\sqrt6))=\frac1{2\sqrt{\frac5{10-\sqrt{5(10+\sqrt{5(8-3\sqrt6)})}}}}

Оба этих страшных равенства следуют из ОТТ

\displaystyle \sqrt[8]{(-8+4\sqrt3\sqrt2)^2+(4\sqrt3\sqrt2)^2}=\sqrt[8]{64-64\sqrt6+96+96}=\sqrt[8]{256-64\sqrt6}

Запишем ответ:

Часть 1:

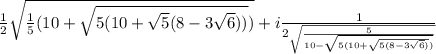
\frac12\sqrt{\frac15(10+\sqrt{5(10+\sqrt5(8-3\sqrt6))})}+i\frac1{2\sqrt{\frac5{10-\sqrt{5(10+\sqrt{5(8-3\sqrt6)})}}}}

Часть 2:

\sqrt[8]{256-64\sqrt6}

ответ: \sqrt[8]{256-64\sqrt6}\left(\frac12\sqrt{\frac15(10+\sqrt{5(10+\sqrt5(8-3\sqrt6))})}+i\frac1{2\sqrt{\frac5{10-\sqrt{5(10+\sqrt{5(8-3\sqrt6)})}}}}\right)Если раскрыть мнимые части, то останется

\sqrt[4]{8\sqrt[4]{-1}\sqrt3-8}

Убирая как тригонометрическую запись, останется только (так как корни и все коэффициенты уйдут под основной корень)

\sqrt[4]{-8+(4+4i)\sqrt6}

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS