абвгдежзи7777

19.09.2020 06:53

Математика

Есть ответ 👍

решить -3.6+4.8*(4 5\6-5 3\4)

268

377

Посмотреть ответы 2

Ответы на вопрос:

oliaputliar

Математика

4,8(62 оценок)

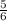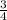-3,6 + 4,8 * (4 $\frac{5}{6}$ - 5 $\frac{3}{4}$ ) = -8

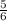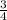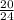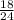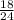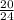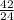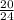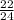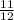
1. 4 $\frac{5}{6}$ - 5 $\frac{3}{4}$ = 4 $\frac{20}{24}$ - 5 $\frac{18}{24}$ = - (5 $\frac{18}{24}$ - 4 $\frac{20}{24}$ ) = - ( 4 $\frac{42}{24}$ - 4 $\frac{20}{24}$ ) = - $\frac{22}{24}$ = - $\frac{11}{12}$

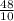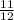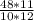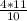2. $\frac{48}{10}$ * (- $\frac{11}{12}$ ) = - $\frac{48 * 11}{10 * 12}$ = - $\frac{4 * 11}{10}$ = - $\frac{44}{10}$ = - 4,4

3. - 3,6 + ( - 4,4) = - 3,6 - 4,4 = -8

3ka9ty1a99

Математика

4,8(22 оценок)

основание данной пирамиды - квадрат. ⇒ ав||сd.

1) если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.

ав || плоскости scd.

2) все точки прямой, параллельной плоскости, равноудалены от этой плоскости. ⇒

расстояние от а до плоскости scd равно расстоянию от любой точки стороны ав до плоскости scd

проведем через высоту пирамиды плоскость мsн ⊥ авсd и || ad.

пирамида правильная, все ее апофемы равны,⇒ треугольник мsн - равнобедренный и основание высоты пирамиды лежит в центре квадрата abcd.

so=4, oh=3 ⇒ ∆ soh - египетский, и sh=5 ( можно найти по т.пифагора)

расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на плоскость.

расстояние от а до плоскости scd равно мк, высоте ∆ мsh, т.е. перпендикуляру, проведенному к sh.

высоту можем найти из площади треугольника.

площадь треугольника равна половине произведения длин высоты и стороны, к которой высота проведена.

s. ∆ мsh=so•mh: 2

s. ∆ мsh=4•6: 2=12

s∆ msh=mk•sh: 2⇒

mk=2s: sh=2•12: 5=4,8 см - это искомое расстояние.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.