Регистрация Спросить otvet5GPT
ЧернаяРадуга
20.11.2021 00:54
Алгебра
Есть ответ 👍

Сколько существует различных распределить между 14 сотрудниками 5 различны(-х, -е) преми(-й, -и)?
Выбери формулу, которой нужно воспользоваться.
ответ .

254
321
Посмотреть ответы 1

Ответы на вопрос:

миша1128
миша1128
4,4(81 оценок)

Объяснение:

а) х=2 это вертикальная асимптота. Это точка разрыва, т. е. это будет та точка, в которой знаменатель равен 0, т.к. на 0 делить нельзя. Следовательно

2·2+b=0;     b=-4

y=3 - это горизонтальная асимптота. К этому значению стремится предел функции. Тогда

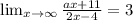
\lim_{x \to \infty} \frac{ax+11}{2x-4} =3

Применяя правило Лопиталя, будем иметь

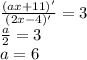
\frac{(ax+11)'}{(2x-4)'} =3\\\frac{a}{2} =3\\a=6

b)

i)

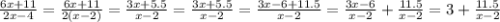
\frac{6x+11}{2x-4}= \frac{6x+11}{2(x-2)}=\frac{3x+5.5}{x-2}=\frac{3x+5.5}{x-2}= \frac{3x-6+11.5}{x-2}= \frac{3x-6}{x-2}+\frac{11.5}{x-2}=3+\frac{11.5}{x-2}

Как видим, к требуемому виду функция не приводится, т.к. 3≠-2

ii) В точках пересечения с осью у абцисса равна 0. Подставляем в уравнение, находим у:

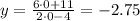
y=\frac{6\cdot0+11}{2\cdot0-4}= -2.75

A(0;-2.75) - точка пересечения с осью у

В точках пересечения с осью х ордината равна 0. Решаем уравнение

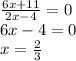
\frac{6x+11}{2x-4}=0\\ 6x-4=0\\x=\frac{2}{3}

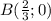B(\frac{2}{3} ;0) - точка пересечения  с осью х.

iii) Дополнительно исследуем функцию в точке разрыва

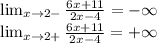
\lim_{x \to 2-} \frac{6x+11}{2x-4}= -\infty\\ \lim_{x \to 2+} \frac{6x+11}{2x-4}= +\infty

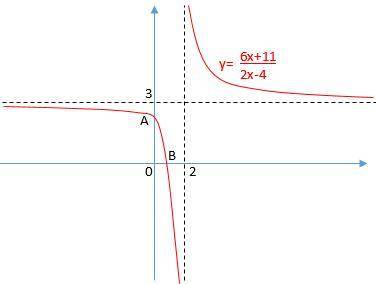
Схематически строим график


Дробно-линейная функция задана уравнением: f(x)=(ax+11)/(2x+b) a) Асимптоты функции имеют уравнения

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS