lerka157

31.10.2022 14:25

Геометрия

Есть ответ 👍

Побудуйте фігуру, в яку перейде трикутник АВС під час повороту навколо вершини С на кут 90° за годинниковою стрілкою

141

257

Посмотреть ответы 2

Ответы на вопрос:

arsenal2108

Геометрия

4,4(36 оценок)

ответ:пррпрпр

прпрпрпрпрп

Объяснение:рпрпр

прпррпрпрпр

PeaceDuck1337

Геометрия

4,8(100 оценок)

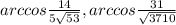
$arccos\frac{14}{5\sqrt{53}}, arccos\frac{31}{\sqrt{3710}}$

Объяснение:

Угол между векторами определяется через их скалярное произведение:

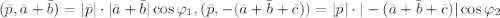
$(\bar{p}, \bar{a}+\bar{b}) = |\bar{p}| \cdot |\bar{a}+\bar{b}| \cos \varphi_1, (\bar{p}, -(\bar{a}+\bar{b}+\bar{c})) = |\bar{p}| \cdot |-(\bar{a}+\bar{b}+\bar{c})| \cos \varphi_2$

Выражаем отсюда косинусы:

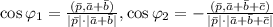
$\cos \varphi_1 = \frac{(\bar{p}, \bar{a}+\bar{b})}{|\bar{p}| \cdot |\bar{a}+\bar{b}|}, \cos \varphi_2 = -\frac{(\bar{p}, \bar{a}+\bar{b}+\bar{c})}{|\bar{p}| \cdot |\bar{a}+\bar{b}+\bar{c}|}$

Считаем скалярные произведения и модули:

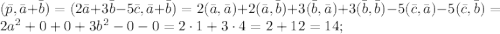
$(\bar{p}, \bar{a}+\bar{b}) = (2\bar{a}+3\bar{b}-5\bar{c}, \bar{a} + \bar{b}) = 2(\bar{a},\bar{a}) + 2(\bar{a},\bar{b}) + 3(\bar{b},\bar{a}) + 3(\bar{b},\bar{b}) -5(\bar{c},\bar{a})-5(\bar{c},\bar{b}) = 2a^2 + 0 + 0 + 3b^2 - 0 - 0 = 2\cdot 1+3\cdot 4 = 2+12 = 14;$

(нулевые скалярные произведения в следствие перпендикулярности векторов). Аналогично:

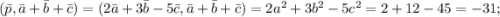
$(\bar p, \bar a + \bar b + \bar c) = (2\bar a + 3\bar b - 5\bar c, \bar a + \bar b + \bar c) = 2a^2 + 3b^2 - 5c^2 = 2 + 12 - 45 = -31;$

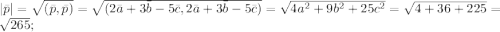
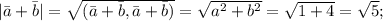
$|\bar p| = \sqrt{(\bar p, \bar p)} = \sqrt{(2\bar a + 3\bar b - 5\bar c, 2\bar a + 3\bar b - 5\bar c)} = \sqrt{4a^2 + 9b^2 + 25c^2} = \sqrt{4+36+225} = \sqrt{265};$ $|\bar a + \bar b| = \sqrt{(\bar a+\bar b, \bar a+\bar b)} = \sqrt{a^2+b^2} = \sqrt{1+4}=\sqrt{5};$

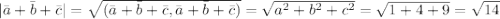
$|\bar a+\bar b+\bar c| = \sqrt{(\bar a+ \bar b + \bar c, \bar a + \bar b + \bar c)} = \sqrt{a^2+b^2+c^2} = \sqrt{1+4+9} = \sqrt{14}$

Подставляем в косинусы:

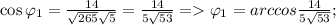
$\cos\varphi_1 = \frac{14}{\sqrt{265}\sqrt{5}} = \frac{14}{5\sqrt{53}} =\varphi_1 = arccos\frac{14}{5\sqrt{53}};$

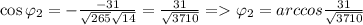
$\cos\varphi_2 = -\frac{-31}{\sqrt{265}\sqrt{14}}= \frac{31}{\sqrt{3710}} = \varphi_2 = arccos\frac{31}{\sqrt{3710}}$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.