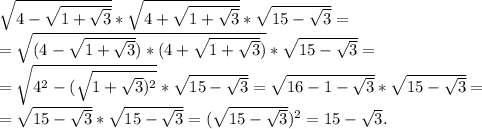Регистрация Спросить otvet5GPT
крошка44
16.11.2021 05:33
Алгебра
Есть ответ 👍

Найдите точку минимума функции y=(х^2-8x+8)eв степени х-6

107
160
Посмотреть ответы 2

Ответы на вопрос:

galaninartem201
galaninartem201
4,5(22 оценок)
Находим производную от функции y'  =  (х^2-8x+8)' e^(x-6) +  (х^2-8x+8)  e^(x-6)' = (2x-8) e^(x-6)  +  (х^2-8x+8)  e^(x-6) = =  e^(x-6) (2x-8+х^2-8x+8) =  e^(x-6) (x^2-6x) находим значения x, при которых производная равна нулю y' = 0 e^(x-6) (x^2-6x) = 0, e^(x-6)> 0, значит  (x^2-6x) = 0,                           x(x-6) = 0,                             x = 0 или x-6 = 0,                                             x = 6   нули производной разбивают область определения производной на промежутки: от минус бесконечности до нуля, от нуля до шести и от шести до плюс бесконечности. (это изображается на числовой оси и отмечается дугаvb)/ определим знак производной на каждом из данных промежутков: при x из промежутка от 6 до плюс бесконечности (допустим x = 10) значение  производной функции больше нуля, при x из промежутка от 0 до 6 (допустим x = 1)  значение  производной меньше нуля,   при x из промежутка от минус бесконечности до нуля (допустим x= -1)  значение  производной функции  больше нуля. при переходе через ноль значение производной меняет знак с плюса на минус, значит точка x = 0 - это точка максимума функции, при переходе через точку 6    значение производной меняет знак с минуса на плюс, значит точка x = 6 - это точка минимума функции. ответ: 6                            
tihomir72
tihomir72
4,8(49 оценок)

Объяснение:

\sqrt{4-\sqrt{1+\sqrt{3} } } *\sqrt{4+\sqrt{1+\sqrt{3} } }*\sqrt{15-\sqrt{3} } =\\ =\sqrt{(4-\sqrt{1+\sqrt{3} } )*(4+\sqrt{1+\sqrt{3} }) } *\sqrt{15-\sqrt{3} } =\\=\sqrt{4^2-(\sqrt{1+\sqrt{3} )^2} } *\sqrt{15-\sqrt{3} } =\sqrt{16-1-\sqrt{3} } *\sqrt{15-\sqrt{3} } =\\=\sqrt{15-\sqrt{3} } *\sqrt{15-\sqrt{3} } =(\sqrt{15-\sqrt{3} } )^2=15-\sqrt{3}.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS