11.08.2021 01:13

Есть ответ 👍

27,6710 0,6781000 23,7100 36,32100 0,00810000 0,021000 7,42100 0,3510 245,3100 0,006810000

295

370

Посмотреть ответы 4

Ответы на вопрос:

bobrikov01

Математика

4,4(90 оценок)

27,67*10=276,7 0,678*1000=678 23,7*100=2370 36,32*100=3632 0,008*10000=80 0,02*1000=207,42*100=742 0,35*10=3,5 245,3*100=24530 0,0068*10000=68

мавштдэкычп

Математика

4,5(1 оценок)

объяснение:

потому что после этих слов идёт определение

Nastyadavydenko

Математика

4,5(80 оценок)

ответ:

каждый звук - шорох птицы, шелест упавшего листа - кажется громким, заставляет опасливо вздрогнуть.

что касается тире перед словом кажется, то здесь всё просто:

если после последнего однородного члена (однородные члены стоят после обобщающего слова) предложение не заканчивается, а продолжается, то после него ставится тире.

однородные члены в предложении - это шорох птицы, шелест упавшего листа. после последнего однородного члена (шелест упавшего листа) предложение продолжается.

поэтому мы должны перед продолжением предложения (кажется громким, заставляет опасливо вздрогнуть) поставить тире.

что касается первого тире, то это авторский знак. по правилам языка после обобщающего слова (звук) и перед однородными членами ставится двоеточие.

по законам языка было бы верно так:

каждый звук : шорох птицы, шелест упавшего листа - кажется громким, заставляет опасливо вздрогнуть.

объяснение:

nazipovadk

Математика

4,7(7 оценок)

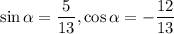
$\sin{\alpha}=\dfrac{5}{13},\cos{\alpha}=-\dfrac{12}{13}$

Пошаговое объяснение:

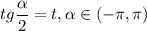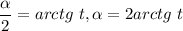Пусть $tg\dfrac{\alpha}{2}=t,\alpha\in (-\pi,\pi)$ . Тогда $\dfrac{\alpha}{2}=arctg\ t, \alpha =2arctg\ t$ .

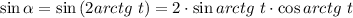
$\sin{\alpha}=\sin{(2arctg\ t)}=2\cdot\sin{arctg\ t}\cdot\cos{arctg\ t}$

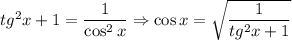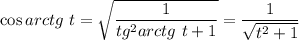
Найдём синус и косинус от арктангенса. Поскольку $tg^2{x}+1=\dfrac{1}{\cos^2{x}}\Rightarrow \cos{x}=\sqrt{\dfrac{1}{tg^2{x}+1}}$ , то $\cos{arctg\ t}=\sqrt{\dfrac{1}{tg^2arctg\ t+1}}=\dfrac{1}{\sqrt{t^2+1}}$

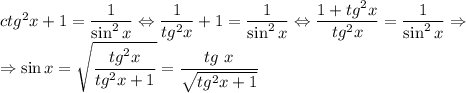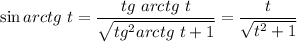Поскольку $ctg^2{x}+1=\dfrac{1}{\sin^2{x}}\Leftrightarrow \dfrac{1}{tg^2{x}}+1=\dfrac{1}{\sin^2{x}}\Leftrightarrow \dfrac{1+tg^2{x}}{tg^2{x}}=\dfrac{1}{\sin^2{x}}\Rightarrow\\\Rightarrow \sin{x}=\sqrt{\dfrac{tg^2{x}}{tg^2{x}+1}}=\dfrac{tg\ x}{\sqrt{tg^2{x}+1}}$ , то $\sin{arctg\ t}=\dfrac{tg\ arctg\ t}{\sqrt{tg^2{arctg\ t}+1}}=\dfrac{t}{\sqrt{t^2+1}}$ .

Получаем: 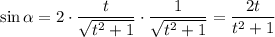$\sin{\alpha}=2\cdot\dfrac{t}{\sqrt{t^2+1}}\cdot\dfrac{1}{\sqrt{t^2+1}}=\dfrac{2t}{t^2+1}$

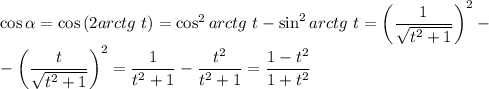
$\cos{\alpha}=\cos{(2arctg\ t)}=\cos^2{arctg\ t}-\sin^2{arctg\ t}=\left(\dfrac{1}{\sqrt{t^2+1}}\right)^2-\\ -\left(\dfrac{t}{\sqrt{t^2+1}}\right)^2=\dfrac{1}{t^2+1}-\dfrac{t^2}{t^2+1}=\dfrac{1-t^2}{1+t^2}$

При t = 5: 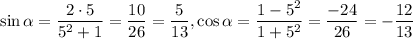$\sin{\alpha}=\dfrac{2\cdot 5}{5^2+1}=\dfrac{10}{26}=\dfrac{5}{13},\cos{\alpha}=\dfrac{1-5^2}{1+5^2}=\dfrac{-24}{26}=-\dfrac{12}{13}$

P. S. Эта замена (через тангенс половинного угла) называется универсальной тригонометрической подстановкой.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.