Докажите если две окружности имеют общую хорду, то прямая, проходящая через центры этих окружностей, перпендикулярна данной хорде.

297

500

Посмотреть ответы 2

Ответы на вопрос:

peindragneel11

Геометрия

4,4(20 оценок)

две точки этой прямой равноудалены от концов хорды. поэтому эта прямая является препендикуляром, проходящим через центр хорды (поскольку все точки, равноудаленные от концов, лежат на этом перпендикуляре).

на самом деле тут часто бывают методические противоречия. дело в том, что когда я учился, нам уже в 5 классе объясняли, что " место точек, равноудаленых от концов отрезка есть прямая, перпендикулярная отрезку и проходящая через его середину". прямая в совпадает с такой прямой в 2 точках, то есть совпадает везде. поэтому доказательство абсолютно точное и простейшее. но сам термин " место точек" может быть не знаком. на самом деле это просто набор точек с заданным свойством. :

MozgVeka

Геометрия

4,4(70 оценок)

1) Объём конуса равен (формула) (1/3)π*R²*h

R - радиус

h - высота

Теорема Пифагора в этом случае: R² + h²=L², выразим R² = (L²- h²) м²

Получилось, что V = (π*( L² - h²)*h)/3 = (π/3)*( L²*h - h³) м³.

Далее: V'(h) = (π/3)*( L² - 3h²). (Это производная)

Нужно прировнять производную к нулю, видим: (π/3)*( L² - 3h²) = 0.

Теперь и второе выражение приравниваем к нулю:

И выражаем: h = √(( L²)/3) = L/√3 = 22,8/√3 примерно равно 4,77493 см.

h у нас положительно число (т.е больше нуля) получается, что: h= (L/√3)! Максимальная!

4,77/√3=(примерно)3.

И нужно подставить значение высоты: h = (L/√3) в уравнение объёма:

V = (π/3)*(L²*(L/√3)-(L/√3)³) = (2π*L3)/(3*√3).

Получаем то, что

V = (2π*22,8*3)/(2/√3) примерно получаем 118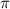 $\pi$ cм³.

ответ: 118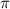 $\pi$

А, если посчитать с числом пи, то получим примерно 371 см²

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.