Регистрация Спросить otvet5GPT
tseng7788
29.01.2020 00:52
Математика
Есть ответ 👍

Кнаименьшему общему знаменателю дроби: а) 1/8 и 3/4 , 9/10и 1/20 , 2/3и 7/12, 7/15и 3/5 б) 1/2 и1/3 ,2/5 и 3/4, 3/16 и 2/3, 1/4и 9/25 в)7/15и 5/9 ,1/6и 3/10 ,5/12 и 7/15 , 7/20 и 7/8 : прошу

201
344
Посмотреть ответы 2

Ответы на вопрос:

Каварныи
Каварныи
4,4(85 оценок)
1/8  и  3/4 = 1/8 и 6/8, 9/10 и 1/20 = 18/20 и 1/20 2/3 и 7/12 = 8/12 и 7/12 7/15 и 3/5 = 7/15 и 9/15 1/2 и 1/3 = 3/6 и 2/6 2/5 и 3/4 = 8/20 и 15/20 3/16 и 2/3 = 9/48 и 32/48 1/4 и 9/25 = 25/100  и 36/100 7/15 и 5/9 = 21/45 и 25/45 1/6 и 3/10 = 5/30 и 9/30 5/12 и 7/15 = 25/60 и 28/60 7/20 и 7/8 = 14/40 и 35/40
mccoy04
mccoy04
4,8(11 оценок)
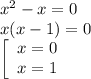
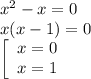
ответ:функция не является непрерывной, в точке х = 0 и х = 1 терпит разрывы первого рода Пошаговое объяснение:Разрыв гарантированно будет в точках где знаменатель равен 0. x^2-x=0\\x(x-1)=0\\\left[\begin{array}{ccc}x=0\\x=1\end{array}\right.

то есть рассматривать будем эти две точки

1. Рассмотрим точку х = 0

1. Тут гарантированно разрыв - делим на 0

2. вычислим односторонние пределы

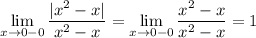
\displaystyle \lim_{x\to0-0} \dfrac{|x^2-x|}{x^2-x}=\lim_{x\to0-0}\dfrac{x^2-x}{x^2-x}=1

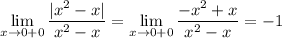
\displaystyle \lim_{x\to0+0} \dfrac{|x^2-x|}{x^2-x}=\lim_{x\to0+0}\dfrac{-x^2+x}{x^2-x}=-1

Разрыв "скачок" - разрыв первого рода

2. Рассмотрим точку х = 1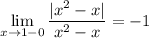

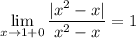
\displaystyle \lim_{x\to1-0} \dfrac{|x^2-x|}{x^2-x}=-1

\displaystyle \lim_{x\to1+0} \dfrac{|x^2-x|}{x^2-x}=1

Тоже самое

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS