TheJurasikBint

13.06.2023 23:24

Есть ответ 👍

Втреугольнике авс прямая mn параллельна стороне ас, делит сторону вс на отрезке bn=15см и nc=5см, а сторону ав на вм и ам. найдите длину отрезка mn, если ас=15см

217

402

Посмотреть ответы 2

Ответы на вопрос:

LadyZed

Геометрия

4,5(80 оценок)

дано:

треугольник авс

mn//ac (параллельно)

bn = 15 см

nc = 5 см

ас = 15 см

найти:

mn - ?

решение:

mn параллельно ac ==> угол bac = углу bmn u угол bnm = углу bca ==> треугольник авс подобен треугольнику mbn ==> mn/ac = bn/bc (пропорция)

вс = bn + nc = 15 + 5 = 20 см

mn/15 = 15/20 =

ответ: mn = 11,25 см

maytanya47

Геометрия

4,4(22 оценок)

AM = 4 см; AC ~ 7,84; R ~ 3 см;

Объяснение:

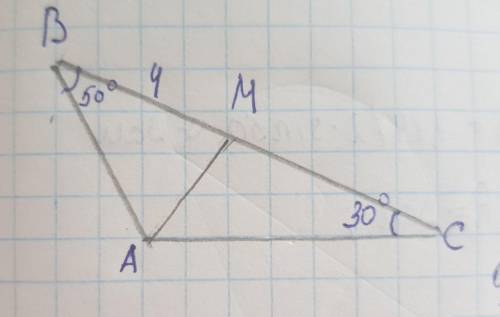
∠BAC =180-B-C =180-50-30 =100

∠BAM =∠BAC/2 =50 (AM - биссектриса ∠BAC)

∠BAM=∠B => △BMA - равнобедренный, AM=BM=4 (см)

б) ∠BМА = 180 - ∠В - ∠ВАМ = 180 - 50 - 50 = 100; ∠АМС смежный углу ∠ВМА, значит ∠АМС = 180 - ∠ВМА = 180 - 80 = 100.

АС ищем через теорему синусов, АМ/sin C = AC/sin AMC => AC = AM*sinAMC/sin C = 4 * sin 100/sin 30 = 8 * sin 100 ~ 8 * 0,98 ~ 7,84см

с) Радиус тоже через теорему синусов.

AC/sinB = 2R => R = AC / 2 * sin B = 7,84 / 2 * sin 50 ~ 3 см

Рисунок прикрепляю

ответ: AM = 4 см; AC ~ 7,84; R ~ 3 см;

Выполнил Барановский Владислав

Можно лучший ответ)

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.