Регистрация Спросить otvet5GPT
vanya498
30.01.2022 22:02
Алгебра
Есть ответ 👍

Если (An) - ариф, прогр. а33=25, а35=33, то а34?

165
287
Посмотреть ответы 1

Ответы на вопрос:

RazzyMatem
RazzyMatem
4,7(39 оценок)

4

Объяснение:

Проверим, является ли левая часть полным дифференциалом некоторой функции u(x, y). Пусть P = x²y² + y, Q = 2x³y - x. Левая часть является полным дифференциалом, если 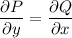\dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x}:

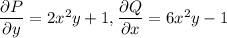
\dfrac{\partial P}{\partial y}=2x^2y+1,\dfrac{\partial Q}{\partial x}=6x^2y-1

Левая часть не является полным дифференциалом. Подберём интегрирующий множитель 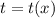t=t(x) такой, чтобы при домножении на него обеих частей уравнения выполнялось равенство 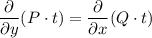\dfrac{\partial}{\partial y}(P\cdot t)=\dfrac{\partial}{\partial x}(Q\cdot t), то есть левая часть стала полным дифференциалом. Так как мы ищем функцию от x, при дифференцировании по y мы считаем её, как константу:

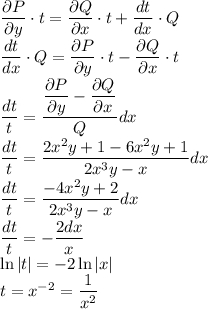
\dfrac{\partial P}{\partial y}\cdot t=\dfrac{\partial Q}{\partial x}\cdot t + \dfrac{dt}{dx}\cdot Q\\\dfrac{dt}{dx}\cdot Q=\dfrac{\partial P}{\partial y}\cdot t-\dfrac{\partial Q}{\partial x}\cdot t\\\dfrac{dt}{t}=\dfrac{\dfrac{\partial P}{\partial y}-\dfrac{\partial Q}{\partial x}}{Q}dx\\\dfrac{dt}{t}=\dfrac{2x^2y+1-6x^2y+1}{2x^3y-x}dx\\\dfrac{dt}{t}=\dfrac{-4x^2y+2}{2x^3y-x}dx\\\dfrac{dt}{t}=-\dfrac{2dx}{x}\\\ln{|t|}=-2\ln|x|\\t=x^{-2}=\dfrac{1}{x^2}

При домножении на t получаем:

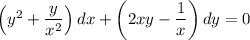
\left(y^2+\dfrac{y}{x^2}\right)dx+\left(2xy-\dfrac{1}{x}\right)dy=0

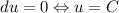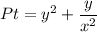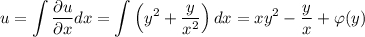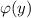Это уравнение в полных дифференциалах. Подберём функцию u(x, y) такую, что du=0\Leftrightarrow u=C. Из определения дифференциала функции двух переменных следует, что Pt=y^2+\dfrac{y}{x^2} — частная производная по x. Тогда \displaystyle u=\int {\dfrac{\partial u}{\partial x}}dx=\int \left(y^2+\dfrac{y}{x^2}\right)dx=xy^2-\dfrac{y}{x}+\varphi (y), где \varphi (y) — константа, зависящая от y (поскольку функция была от двух переменных, а проинтегрировали мы только по x). Также из определения дифференциала:

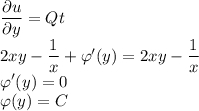
\dfrac{\partial u}{\partial y}=Qt\\2xy-\dfrac{1}{x}+\varphi'(y)=2xy-\dfrac{1}{x}\\\varphi'(y)=0\\\varphi(y)=C

Тогда 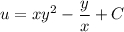u=xy^2-\dfrac{y}{x}+C, решение уравнения: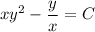 xy^2-\dfrac{y}{x}=C

При x = 1, y = 1 получаем C = 0. Выразим y через x:

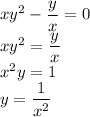
xy^2-\dfrac{y}{x}=0\\xy^2=\dfrac{y}{x}\\x^2y=1\\y=\dfrac{1}{x^2}

В точке 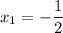x_1=-\dfrac{1}{2} значение функции равно 4.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS