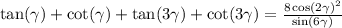Ответы на вопрос:
Например, система уравнений может быть задана следующим образом.
x + 5y = 7
3x − 2y = 4
Чтобы решить систему уравнений, нужно найти и «x», и «y».
Разберем подстановки на примере.
x + 5y = 7
3x − 2y = 4
Выразим из первого уравнения «x + 5y = 7» неизвестное «x».
Перенесём в первом уравнении «x + 5 y = 7» всё что содержит «x» в левую часть, а остальное в правую часть по правилу переносу.
При «x» стоит коэффициент равный единице, поэтому дополнительно делить уравнение на число не требуется.
x = 7 − 5y
3x − 2y = 4
Теперь, вместо «x» подставим во второе уравнение полученное выражение
«x = 7 − 5y» из первого уравнения.
x = 7 − 5y
3(7 − 5y) − 2y = 4
Подставив вместо «x» выражение «(7 − 5y)» во второе уравнение, мы получили обычное линейное уравнение с одним неизвестным «y». Решим его по правилам решения линейных уравнений.
Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение «3(7 − 5y) − 2y = 4» отдельно. Вынесем его решение отдельно с обозначения звездочка (*).
x = 7 − 5y
3(7 − 5y) − 2y = 4 (*)
(*) 3(7 − 5y) − 2y = 4
21 − 15y − 2y = 4
− 17y = 4 − 21
− 17y = − 17 | :(−17)
y = 1
Мы нашли, что «y = 1». Вернемся к первому уравнению «x = 7 − 5y» и вместо «y» подставим в него полученное числовое значение. Таким образом можно найти «x». Запишем в ответ оба полученных значения.
x = 7 − 5y
y = 1
x = 7 − 5 · 1
y = 1
x = 2
y = 1
ответ: x = 2; y = 1
сложения
Рассмотрим другой решения системы уравнений. Метод называется сложения. Вернемся к нашей системе уравнений еще раз.
x + 5y = 7
3x − 2y = 4
По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные уравнения, получить такое уравнение, в котором останется только одно неизвестное.
Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
4. Упростите выражение (6х-х2)2 -х2 (х – 1)(х+1) + 6x (3 + 2x2)....
 curlyprettygirl14.12.2022 05:25
curlyprettygirl14.12.2022 05:25 -
Упростите выражение а)1/cos²A-1 б)1/sin²A-1 за не правильный ответ бан жалоба..за...
 vitalik231203114.03.2021 19:17
vitalik231203114.03.2021 19:17 -
расписать всё подробно...
 UliaAndKisas27.11.2021 02:39
UliaAndKisas27.11.2021 02:39 -
Алгебра линейное уравнение решите x+у-6=24...
 karinaandreevozb5ha05.12.2020 20:20
karinaandreevozb5ha05.12.2020 20:20 -
(3x + y) + (y – 3x+ 2y+2x)=...
 ggggdcdxf30.06.2020 20:49
ggggdcdxf30.06.2020 20:49 -
Ломаная ABC - график некоторой функции, причем Начертите график и найдите по...
 rasaka12325.09.2021 03:43
rasaka12325.09.2021 03:43 -
А)а2/3а-6 - 4/3а-6 б)5x/x-y*x2-y2/10x3...
 cyganka8406.11.2022 20:31
cyganka8406.11.2022 20:31 -
Функция задана формулой y=-5x+10 определите чему равен y при х=2,5 (начертите...
 ashbringer1233201.05.2021 15:10
ashbringer1233201.05.2021 15:10 -
Жауабы: y=2x y=-2x y=x+1...
 мамадочп4а15.11.2022 01:41
мамадочп4а15.11.2022 01:41 -
1) (x+y) ^2 = (x+y) (x+y) = 2) (5a+1) ^2= 3) (m-3) ^3= 4) (1-b) ^2= 5) (x-1)...
 PaulinaWalters10.04.2021 09:39
PaulinaWalters10.04.2021 09:39

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.