Алгебра: Будь ласка знайдіть x0 до функції дотичної

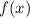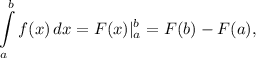
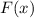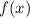
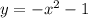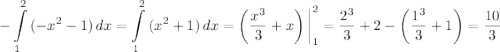
Чтобы вычислить площадь фигуры, ограниченной графиком функции на заданном промежутке , следует найти определенный интеграл: где — первообразная для функции 1) Имеем функцию и следует вычислить площадь, которую она ограничивает на координатной плоскости на отрезке Найдем определенный интеграл, приписав перед ним знак минус , поскольку график функции находится под осью абсцисс:2) Вычислим площадь фигуры, ограниченной графиками функци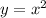й и 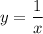на отрезке Чтобы найти эту площадь, следует вычислить определенный...

bagfaver

03.01.2021 09:21

Алгебра

Есть ответ 👍

Будь ласка знайдіть x0 до функції дотичної

223

329

Посмотреть ответы 1

Ответы на вопрос:

scapper

Алгебра

4,7(22 оценок)

Чтобы вычислить площадь фигуры, ограниченной графиком функции f(x) на заданном промежутке $[a; \ b]$ , следует найти определенный интеграл:

$\displaystyle \int\limits^b_a {f(x)} \, dx = F(x) |^{b}_{a} = F(b) - F(a),$

где F(x) — первообразная для функции f(x)

1) Имеем функцию $y = -x^{2} - 1$ и следует вычислить площадь, которую она ограничивает на координатной плоскости на отрезке $[1; \ 2]$

Найдем определенный интеграл, приписав перед ним знак "минус", поскольку график функции находится под осью абсцисс:

$-\displaystyle \int\limits^2_1 {(-x^{2} - 1)} \, dx = \int\limits^2_1 {(x^{2} + 1)} \, dx = \left(\dfrac{x^{3}}{3} + x \right) \bigg| ^{2}_{1} = \dfrac{2^{3}}{3} + 2 - \left(\dfrac{1^{3}}{3} + 1 \right) = \dfrac{10}{3}$

2) Вычислим площадь фигуры, ограниченной графиками функций $y = x^{2}$ и $y = \dfrac{1}{x}$ на отрезке $[1; \ 3]$

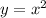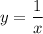Чтобы найти эту площадь, следует вычислить определенный интеграл разности функций $y = x^{2}$ и $y = \dfrac{1}{x}$ (только при такой разности площадей, образованных функциями на координатной плоскости, получим площадь фигуры, изображенной на рисунке):

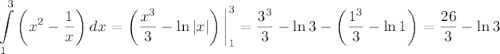
$\displaystyle \int\limits^3_1 {\left(x^{2} - \dfrac{1}{x} \right)} \, dx = \left(\dfrac{x^{3}}{3} - \ln |x| \right)\bigg|^{3}_{1} = \dfrac{3^{3}}{3} - \ln 3 - \left(\dfrac{1^{3}}{3} - \ln 1 \right) = \dfrac{26}{3} - \ln 3$

ответ: 1) 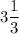$3\dfrac{1}{3}$ кв. ед.; 2) 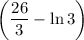$\left( \dfrac{26}{3} - \ln 3 \right)$ кв. ед.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.