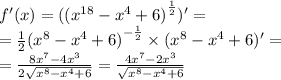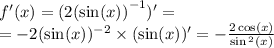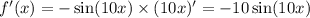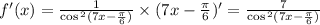Ответы на вопрос:
Рискну предположить: xlv=45 lx=60 dccl=750 xxx=30 xcix=99 подставляя значения получаем: 45•60+750: 30-99=2700+25-99=2626 2626= mmdcxxvi
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Сейчас др сегодняшней полуночи осталось вдвое больше времент,чем 8 часов назад...
 помоги136101.04.2022 09:12
помоги136101.04.2022 09:12 -
Используя данные отрезки построй отрезок длинна которого равна 1 дмитрий...
 Askemba06.06.2020 20:14
Askemba06.06.2020 20:14 -
Втреугольнике одна из сторон равна 12 а другая равна 16 а синус угла между...
 Seasons120.08.2021 20:50
Seasons120.08.2021 20:50 -
Какое числочисло надо умножить на 42 чтобы получить разность чисел 500 и 38...
 Nastykissa02.01.2022 20:25
Nastykissa02.01.2022 20:25 -
Два теплохода вышли из двух портов на встречу друг другу .первый проходил 180кл...
 егор2357858428.12.2020 20:00
егор2357858428.12.2020 20:00 -
В2ящиках 85 кг моркови.после того как из каждого ящика взяли одинаковое количество...
 Руслик11111111101.05.2021 07:47
Руслик11111111101.05.2021 07:47 -
Веревку длиной 20 метров разрезали на 3 равные части какова длина каждой части...
 малина10625.11.2021 08:06
малина10625.11.2021 08:06 -
Вася 27 февраля 2012 года в 19-35 начал готовится к поступлению в фмл № 239...
 залина06114.01.2022 01:05
залина06114.01.2022 01:05 -
Пренадлежит ли графику уравнения 17×(-3)+24×2,5=-15 точка а(-3; 2,5)...
 БЕРЕНА20.01.2022 09:31
БЕРЕНА20.01.2022 09:31 -
Решить велосипедисту необходимо преодолеть путь ,состоящий из трёх участков...
 Маслинка17411.04.2021 05:48
Маслинка17411.04.2021 05:48

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.