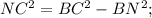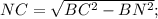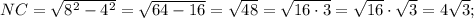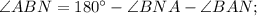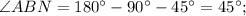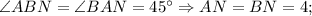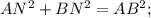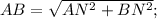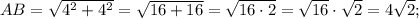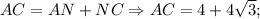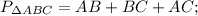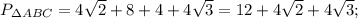Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Геометрия
-
Рисовать не надо только решите и всё...
 natchiy0314.10.2021 21:32
natchiy0314.10.2021 21:32 -
1. В кубе точки , середины рёбер соответственно и . Найдите косинус...
 gtagiev18.12.2020 14:19
gtagiev18.12.2020 14:19 -
Решите эти 3 задачи на листиках и нарисуйте чертежи для каждой...
 AnyaFilenkova17.12.2022 22:06
AnyaFilenkova17.12.2022 22:06 -
1). В прямоугольном треугольнике АВС А = 90°, АВ = 20 см; высота...
 azimova011314.10.2022 06:11
azimova011314.10.2022 06:11 -
Ребята , мне нужно 1 вариант ПОДЧЕРКНИТЕ ОШИБОЧНОЕ УТВЕРЖДЕНИЕ...
 bertain08.05.2022 17:24
bertain08.05.2022 17:24 -
Точки А, В, С лежать на одній прямій. Чи лежить точка С між точками...
 netunikaa29.07.2022 12:19
netunikaa29.07.2022 12:19 -
Что за угол, градусная мера, которого равна 67°?...
 awdrg1234518.02.2022 07:46
awdrg1234518.02.2022 07:46 -
Доведіть, що основи трапеції гомотетичні відносно точки перетину...
 adidas296302.05.2022 20:00
adidas296302.05.2022 20:00 -
Відрізок OS проведено з центра O квадрата ABCD перпенди- кулярно...
 Dimn1117.03.2022 11:38
Dimn1117.03.2022 11:38 -
Укажіть назву природної зони, де ростуть динне, хлібне, червоне...
 Zara221730.04.2023 07:12
Zara221730.04.2023 07:12

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.