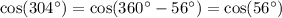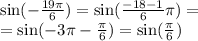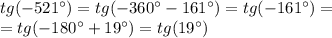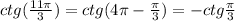Регистрация Спросить otvet5GPT
ali6619
21.03.2022 19:07
Алгебра
Есть ответ 👍

Приведите тригонометрическую функцию произвольного аргумента к тригонометрической функции острого угла:
cos304°, sin ( - 19 пи /6),tg(-521°),ctg 11пи/3)

230
364
Посмотреть ответы 2

Ответы на вопрос:

cyrkunova56
cyrkunova56
4,5(77 оценок)

\cos(304^{\circ}) = \cos(360 ^{\circ}- 56^{\circ}) = \cos(56^{\circ})

\sin( - \frac{19\pi}{6} ) = \sin( \frac{ - 18 - 1}{6}\pi ) = \\ = \sin( - 3\pi - \frac{\pi}{6} ) = \sin( \frac{\pi}{6} )

tg( - 521^{\circ}) = tg( - 360^{\circ} - 161^{\circ}) = tg( - 161^{\circ}) = \\ = tg( - 180^{\circ} + 19^{\circ}) = tg(19^{\circ})

ctg( \frac{11\pi}{3} ) = ctg(4\pi - \frac{\pi}{3} ) = - ctg \frac{\pi}{ 3} \\

yuhdbfbgg
yuhdbfbgg
4,5(41 оценок)
Для  начала напишем одз: х+1≠0 и х+2≠0, значит х≠-1 и х≠-2 данное уравнение может иметь два корня один корень уравнение имеет в следующих случаях: 1 случайа=-а 2а=0 а=0 2 случай  один из корней числителя равен одному из корней знаменателя: х+а=х+1 а=1 3 случай х+а=х+2 а=2 4 случай х-а=х+1 а=-1 5 случай х-а=х+2 а=-2 при всех данных а уравнение имеет 1 корень. отв: а=0; а=1; а=-1; а=2; а=-2  в этом можно убедиться: 1)пусть а=0, тогда x²=0 x=0 -1 корень 2) пусть а=1, тогда  x-1=0 x=1 - 1 корень 3) пусть а=-1, тогда  x-1=0 x=1 - 1 корень4) а=2 х-2=0 х=2 - 1 корень 5) а=-2 х-2=0 х=2 - 1 корень

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS