Математика: Решите систему уравнений

slavik528

01.10.2022 06:00

Математика

Есть ответ 👍

Решите систему уравнений

212

243

Посмотреть ответы 2

Ответы на вопрос:

BloodRainbow

Математика

4,6(32 оценок)

23,2

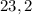
Пошаговое объяснение:

ОДЗ:

$x \neq 0, \quad y \neq 0;$

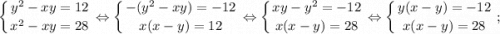
$\displaystyle \left \{ {{y^{2}-xy=12} \atop {x^{2}-xy=28}} \right. \Leftrightarrow \left \{ {{-(y^{2}-xy)=-12} \atop {x(x-y)=12}} \right. \Leftrightarrow \left \{ {{xy-y^{2}=-12} \atop {x(x-y)=28}} \right. \Leftrightarrow \left \{ {{y(x-y)=-12} \atop {x(x-y)=28}} \right. ;$

Разделим верхнее уравнение на нижнее:

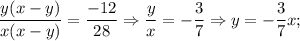
$\dfrac{y(x-y)}{x(x-y)}=\dfrac{-12}{28} \Rightarrow \dfrac{y}{x}=-\dfrac{3}{7} \Rightarrow y=-\dfrac{3}{7}x;$

Подставим полученное значение "у" в исходное уравнение:

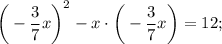
$\bigg (-\dfrac{3}{7}x \bigg )^{2}-x \cdot \bigg (-\dfrac{3}{7}x \bigg )=12;$

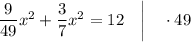
$\dfrac{9}{49}x^{2}+\dfrac{3}{7}x^{2}=12 \quad \bigg | \quad \cdot 49$

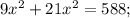
$9x^{2}+21x^{2}=588;$

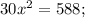
$30x^{2}=588;$

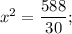
$x^{2}=\dfrac{588}{30};$

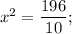
$x^{2}=\dfrac{196}{10};$

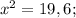
$x^{2}=19,6;$

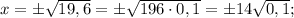
$x=\pm \sqrt{19,6}=\pm \sqrt{196 \cdot 0,1}=\pm 14\sqrt{0,1};$

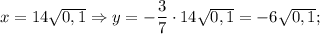
$x=14\sqrt{0,1} \Rightarrow y=-\dfrac{3}{7} \cdot 14\sqrt{0,1}=-6\sqrt{0,1};$

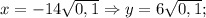
$x=-14\sqrt{0,1} \Rightarrow y=6\sqrt{0,1};$

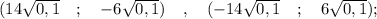
$(14\sqrt{0,1} \quad ; \quad -6\sqrt{0,1}) \quad , \quad (-14\sqrt{0,1} \quad ; \quad 6\sqrt{0,1});$

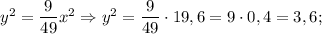
$y^{2}=\dfrac{9}{49}x^{2} \Rightarrow y^{2}=\dfrac{9}{49} \cdot 19,6=9 \cdot 0,4=3,6;$

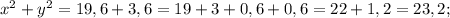
$x^{2}+y^{2}=19,6+3,6=19+3+0,6+0,6=22+1,2=23,2;$

Лавданим

Математика

4,4(29 оценок)

То та наклонная больше, у которой проекция будет больше. то угол между наклонной и плоскостью будет измеряться как угол между наклонной и её проекцией на эту плоскость.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.