Регистрация Спросить otvet5GPT
AKA1111173
03.10.2022 09:32
Математика
Есть ответ 👍

Используя свойства неравенств, запишите верное неравенство, которое получится если к обеим частям неравентсва 3a - 5 > 2а - 1 прибавить число 7; 4а; -3; -2а;​

102
113
Посмотреть ответы 2

Ответы на вопрос:

sir228qwerty
sir228qwerty
4,5(69 оценок)

ОтвеДано: 3a-5>2a-1

прибавляем по порядку

1) 3a-5+7>2a-1+7

3a+2>2a+6

2) 3a-5+4a>2a-1+4a

7a-5>6a-1

3) 3a-5+(-3)>2a-1+(-3)

3a-5-3>2a-1-3

3a-8>2a-4

4) 3a-5+2a>2a-1+2a

5a-5>4a-1

Дано: 3.2m-2.4<5.6m-1.6

умножаем по порядку

1) (3.2m-2.4)*5<(5.6m-1.6)*5

16m-12<28m-8

2) (3.2m-2.4)*1/2<(5.6m-1.6)*1/2

1.6m-1.2<2.8m-0.8

3) (3.2m-2.4)*1/4<(5.6m-1.6)*1/4

0.8m-0.6<1.4m-0.4т:

Пошаговое объяснение:

givka1
givka1
4,4(22 оценок)

Наибольший возможный объем цилиндра равен 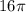16\pi

Пошаговое объяснение:

Пусть радиус основания цилиндра равен 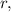r, а высота — 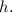h. Тогда площадь боковой поверхности равна 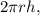2\pi rh, а сумма площадей верхнего и нижнего оснований —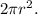 2\pi {r^2}.

По условию задачи

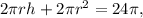
2\pi rh + 2\pi {r^2} = 24\pi,

откуда удобно выразить высоту:

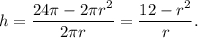
h = \displaystyle\frac{{24\pi - 2\pi {r^2}}}{{2\pi r}} = \displaystyle\frac{{12 - {r^2}}}{{r}}.

Объем цилиндра

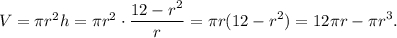
V = \pi {r^2}h = \pi {r^2} \cdot \displaystyle\frac{{12 - {r^2}}}{{r}} = \pi r(12 - {r^2}) = 12\pi r - \pi {r^3}.

Исследуем функцию 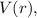V(r), найдем ее производную:

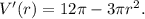
V'(r) = 12\pi - 3\pi {r^2}.

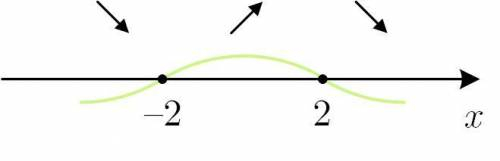
Уравнение 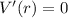V'(r) = 0 дает корни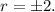 r = \pm 2.

С метода интервалов убеждаемся, что 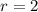r = 2 является максимумом этой функции.

Тогда значение объема, соответствующего этому радиусу, равно

V(2) = 12\pi\cdot2-\pi\cdot8=16\pi.


Найти наибольший возможный объём цилиндра, площадь полной поверхности которого равна 24л.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS