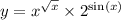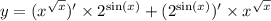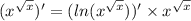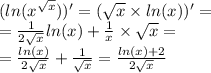Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
С объяснением и решением Три волка съедает 2 овец за 40 минут. За сколько минут...
 Kfhjrhnf12.12.2022 00:47
Kfhjrhnf12.12.2022 00:47 -
Определи цифру которую можно поставить всмето * чтобы число 45 *46 делилось на...
 Алиналабвдк12.02.2022 06:00
Алиналабвдк12.02.2022 06:00 -
Нок(25;35) =? Нод(25;35)...
 Баянсулу1123.09.2021 23:40
Баянсулу1123.09.2021 23:40 -
Карлсон за 10 дней съел 40 л варенья Сколько литров он съедал за 1 день если каждый...
 linagalkinaa108.11.2022 22:41
linagalkinaa108.11.2022 22:41 -
Вычислите: ac и bd если a/b=c/d и a*b*c*d=900...
 Unicorn47122.03.2022 02:45
Unicorn47122.03.2022 02:45 -
Вступительные испытания...
 Malika27406.06.2023 11:27
Malika27406.06.2023 11:27 -
Точка ПО закону Материальная движется прямолинейно х(t)= 2t^3 +t^2 - 5t + 98,...
 герман13630.01.2021 06:51
герман13630.01.2021 06:51 -
Из 100 кг молока получается 8 кг сыра. Сколько килограмм молока нужно для приготовления...
 Uliana700321.12.2022 10:53
Uliana700321.12.2022 10:53 -
решить уровнение, заранее...
 kotenok8806.08.2021 19:43
kotenok8806.08.2021 19:43 -
Согнув пролволку сделали равносторонний треугольник со стороной 16 см, потом из...
 eroly12ramblerr212.05.2020 01:42
eroly12ramblerr212.05.2020 01:42

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.