Регистрация Спросить otvet5GPT
julss11
15.08.2020 09:44
Алгебра
Есть ответ 👍

В треугольнике ABC AC=BC, AB=10, cosA=0,6. Найдите высоту AH

120
374
Посмотреть ответы 3

Ответы на вопрос:

alievvusal57vusal
alievvusal57vusal
4,5(41 оценок)

АН=8

Объяснение:

В треугольнике АВС известно:

АС = ВС;

АВ = 10;

cos А = 0,6.

Найдем высоту АН.

Так как, треугольник равнобедренный, тогда cos A = cos B = 0.6.

Рассмотрим прямоугольный треугольник АНВ с прямым углом Н.

sin B = √(1 - cos^2 B) = √(1 - 0.6^2) = √(1 - 0.36) = √0.64 = 0.8;

sin B = AH/AB;

Выразим отсюда высоту АН.

АН = АВ * sin a;

Подставим известные значения в формулу и вычислим значение высоты треугольника АВС.

АН = 10 * 0.8 = 8;

В итоге получили, что высота треугольника АВС равна АН = 8.

ответ: АН = 8.

tori0077
tori0077
4,6(49 оценок)

решение на фотографии


В треугольнике ABC AC=BC, AB=10, cosA=0,6. Найдите высоту AH
милана200229
милана200229
4,4(94 оценок)

Есть известная формула так называемая формула дополнительного угла (в интернете можете почитать об этом). Запишу кратко формулу:

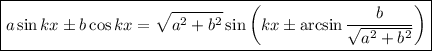
\boxed{a\sin kx\pm b\cos kx=\sqrt{a^2+b^2}\sin\left(kx\pm\arcsin\frac{b}{\sqrt{a^2+b^2}}\right)}

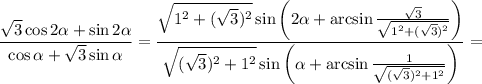
\dfrac{\sqrt{3}\cos2\alpha+\sin2\alpha}{\cos\alpha+\sqrt{3}\sin\alpha}=\dfrac{\sqrt{1^2+(\sqrt{3})^2}\sin\left(2\alpha+\arcsin\frac{\sqrt{3}}{\sqrt{1^2+(\sqrt{3})^2}}\right)}{\sqrt{(\sqrt{3})^2+1^2}\sin\left(\alpha+\arcsin\frac{1}{\sqrt{(\sqrt{3})^2+1^2}}\right)}=

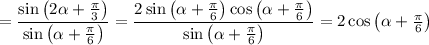
=\dfrac{\sin\left(2\alpha+\frac{\pi}{3}\right)}{\sin\left(\alpha+\frac{\pi}{6}\right)}=\dfrac{2\sin\left(\alpha+\frac{\pi}{6}\right)\cos\left(\alpha+\frac{\pi}{6}\right)}{\sin\left(\alpha+\frac{\pi}{6}\right)}=2\cos\left(\alpha+\frac{\pi}{6}\right)

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS