Докажите, что биссектрисы углов прямоугольника своим
пересечением образуют квадрат. С чертежом

101

157

Посмотреть ответы 2

Ответы на вопрос:

Tania22012003

Геометрия

4,5(96 оценок)

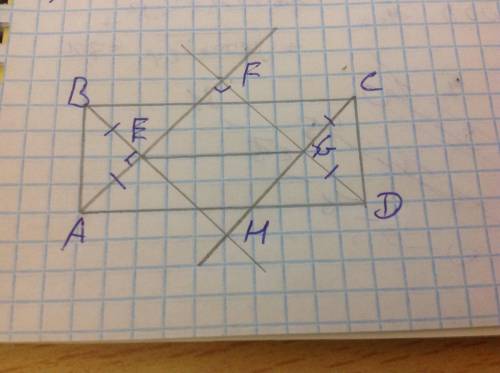
Пусть в прямоугольнике ABCD биссектрисы пересекаются в точках E,F,G,H. Докажем, что EFGH - квадрат. В треугольнике AFD углы A и D равны 45 градусам, тогда угол F равен 90 градусам. Аналогично, в треугольнике BCH углы B и C равны 45 градусам, а угол H равен 90 градусам. В треугольнике ABE углы A и B равны 45 градусам, тогда угол E равен 90 градусам. Тогда и угол FEH равен 90 градусам (вертикальные углы равны). Аналогично, в треугольнике CDG углы C и D равны 45 градусам, тогда угол G равен 90 градусам и угол FGH равен 90 градусам. Таким образом, все углы четырехугольника EFGH равны 90 градусам и этот четырехугольник является прямоугольником.

Теперь докажем, что соседние стороны EF и FG этого прямоугольника равны. Треугольники ABE и CDG равны, так как каждый из них - равнобедренный и прямоугольный и их гипотенузы равны. Тогда AE=DG. Треугольник ADF является равнобедренным и прямоугольным, тогда AF=DF. Тогда EF=AF-AE, GF=DF-DG, откуда EF=GF, треугольник EFG равнобедренный и EF=FG. Так как в прямоугольнике EFGH соседние стороны равны, этот прямоугольник - квадрат, что и требовалось доказать.

Объяснение:

Докажите, что биссектрисы углов прямоугольника своим пересечением образуют квадрат. С чертежом

notty12

Геометрия

4,7(83 оценок)

*********************** вывести формулу не удалось но доказать справедливость формулы - получилось

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.