Регистрация Спросить otvet5GPT
yanarem1
04.09.2022 04:06
Алгебра
Есть ответ 👍

Решить уравнения тригонометрия ( )

181
284
Посмотреть ответы 2

Ответы на вопрос:

abdrahmanovamir123
abdrahmanovamir123
4,4(26 оценок)

1.

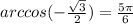
arccos( - \frac{ \sqrt{3} }{2} ) = \frac{5\pi}{6} \\

2.

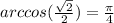
arccos( \frac{ \sqrt{2} }{2} ) = \frac{\pi}{4} \\

3.

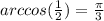
arccos( \frac{1}{2} ) = \frac{\pi}{3} \\

4.

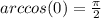
arccos(0) = \frac{\pi}{2} \\

5.

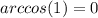
arccos(1) = 0 \\

6.

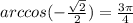
arccos( - \frac{ \sqrt{2} }{2} ) = \frac{3\pi}{4} \\

7.

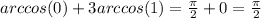
arccos(0) + 3arccos(1) = \frac{\pi}{2} + 0 = \frac{\pi}{2} \\

8.

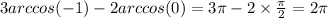
3arccos( - 1) - 2arccos(0) = 3\pi - 2 \times \frac{\pi}{2} = 2\pi \\

9.

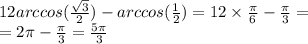
12arccos( \frac{ \sqrt{3} }{2} ) - arccos( \frac{1}{2} ) = 12 \times \frac{\pi}{6} - \frac{\pi}{3} = \\ = 2\pi - \frac{\pi}{3} = \frac{5\pi}{3}

10.

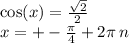
\cos(x) = \frac{ \sqrt{2} }{2} \\ x = + - \frac{\pi}{4} + 2\pi \: n

11.

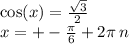
\cos(x) = \frac{ \sqrt{3} }{2} \\ x = + - \frac{\pi}{6} + 2 \pi \: n

12.

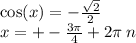
\cos(x) = - \frac{ \sqrt{2} }{2} \\ x = + - \frac{3\pi}{4} + 2\pi \: n

13.

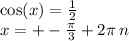
\cos(x) = \frac{1}{2} \\ x = + - \frac{\pi}{3} + 2\pi \: n

14.

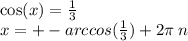
\cos(x) = \frac{1}{3} \\ x = + - arccos( \frac{1}{3} ) + 2\pi \: n

15.

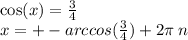
\cos(x) = \frac{3}{4} \\ x = + - arccos( \frac{3}{4} ) + 2\pi \: n

16.

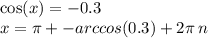
\cos(x) = - 0.3 \\ x = \pi + - arccos(0.3) + 2\pi \: n

17.

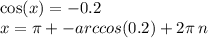
\cos(x) = - 0.2 \\ x = \pi+ - arccos(0.2) + 2\pi \: n

18.

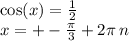
\cos(x ) = \frac{1}{2} \\ x = + - \frac{ \pi}{3} + 2\pi \: n

19.

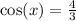
\cos(x) = \frac{4}{3} \\

нет корней, так как

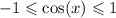
- 1 \leqslant \cos(x) \leqslant 1

везде n принадлежит Z.

Mimi67392
Mimi67392
4,4(83 оценок)

Уравнением.

Пусть 17x-мужчины, тогда женщины 18x. Зная общее количество людей, составим и решим уравнение.

17x+18x=700

35x=700

x=700/35

x=20. Зная x, найдем кол-во  женщин

2)20*18=360(женщин)

ответ: 360

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS