Регистрация Спросить otvet5GPT
neleachibzii
03.11.2022 19:11
Алгебра
Есть ответ 👍

Две семьи отправились на детский утренник. Первая семья купила два детских билета и один взрослый и всего заплатила 495 рублей. Вторая семья купила три детских билета и два взрослых и всего заплатила 850 рублей. Сколько стоит один детский билет и сколько стоит один взрослый билет?

141
467
Посмотреть ответы 1

Ответы на вопрос:

alik781
alik781
4,6(46 оценок)

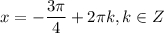
x=-\dfrac{3\pi}{4}+2\pi k, k\in Z

Объяснение:

Заметим:

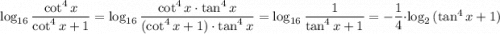
1) \log_{16}{\dfrac{\cot^4x}{\cot^4x+1}}=\log_{16}{\dfrac{\cot^4x\cdot \tan^4 x}{(\cot^4x+1)\cdot \tan^4 x}}=\log_{16}{\dfrac{1}{\tan^4 x+1}}=-\dfrac{1}{4}\cdot \log_{2}{(\tan^4 x+1)}

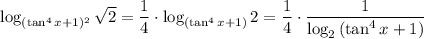
2) \log_{(\tan^4x+1)^2}\sqrt{2}=\dfrac{1}{4}\cdot \log_{(\tan^4x+1)}2=\dfrac{1}{4}\cdot \dfrac{1}{\log_{2}{(\tan^4 x+1)}}

Уравнение перепишем в виде

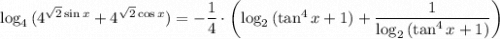\log_4{(4^{\sqrt{2}\sin x}+4^{\sqrt{2}\cos x})}=-\dfrac{1}{4}\cdot \left(\log_{2}{(\tan^4 x+1)}+\dfrac{1}{\log_{2}{(\tan^4 x+1)}} \right). При этом (основание логарифма не равно 1) 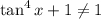\tan ^4x +1\neq 1. Тогда верна цепочка неравенств

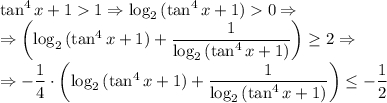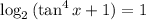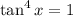\tan^4 x+1 1\Rightarrow \log_{2}{(\tan^4 x+1)} 0\Rightarrow \\ \Rightarrow\left(\log_{2}{(\tan^4 x+1)}+\dfrac{1}{\log_{2}{(\tan^4 x+1)}} \right) \geq 2\Rightarrow \\ \Rightarrow-\dfrac{1}{4}\cdot \left(\log_{2}{(\tan^4 x+1)}+\dfrac{1}{\log_{2}{(\tan^4 x+1)}} \right) \leq -\dfrac{1}{2}, причем равенство может достигаться лишь при \log_{2}{(\tan^4 x+1)}=1, т.е. при \tan^4 x=1.

Оценим теперь левую часть полученного уравнения.

По неравенству о средних верно

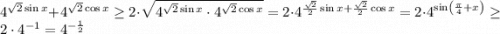
4^{\sqrt{2}\sin x}+4^{\sqrt{2}\cos x}\geq 2\cdot \sqrt{4^{\sqrt{2}\sin x}\cdot 4^{\sqrt{2}\cos x}}=2\cdot 4^{\frac{\sqrt{2}}{2}\sin x+\frac{\sqrt{2}}{{2}}\cos x}=2\cdot 4^{\sin\left(\frac{\pi}{4}+x\right)}\geq 2\cdot 4^{-1}=4^{-\frac{1}{2}}

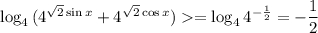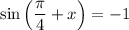Отсюда (т.к. основание 4 логарифма больше 1) верна оценка \log_4{(4^{\sqrt{2}\sin x}+4^{\sqrt{2}\cos x})} =\log_4{4^{-\frac{1}{2}}}=-\dfrac{1}{2}, причем равенство может достигаться лишь при \sin\left(\dfrac{\pi}{4}+x\right)=-1.

Значит, решение уравнения эквивалентно решению системы

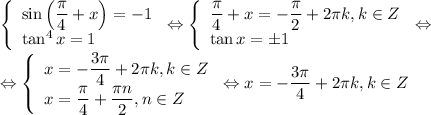
\left\{\begin{array}{l}\sin\left(\dfrac{\pi}{4}+x\right)=-1\\\tan^4 x=1\end{array}\right.\Leftrightarrow \left\{\begin{array}{l}\dfrac{\pi}{4}+x=-\dfrac{\pi}{2}+2\pi k, k\in Z\\\tan x=\pm1\end{array}\right.\Leftrightarrow \\\Leftrightarrow\left\{\begin{array}{l}x=-\dfrac{3\pi}{4}+2\pi k, k\in Z\\x=\dfrac{\pi}{4}+\dfrac{\pi n}{2}, n\in Z\end{array}\right.\Leftrightarrow x=-\dfrac{3\pi}{4}+2\pi k, k\in Z

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS