Регистрация Спросить otvet5GPT
arven88
22.01.2020 05:32
Геометрия
Есть ответ 👍

Напиши уравнение окружности, которая проходит через точку 8 на оси Ox и через точку 6 на оси Oy, если известно, что центр находится на оси Ox. (Рассчитай в дробях и дроби запиши несокращёнными.)

(x- )^2+y^2=(дробь)^2

134
214
Посмотреть ответы 2

Ответы на вопрос:

sasha123123476
sasha123123476
4,6(10 оценок)

(х-х₀)²+(y-y₀)²=R² - уравнение окружности в общем виде

Окружность проходит через точки (6;0) и (0;8), следовательно,

х=6; y=8;

Центр окружности (x₀;y₀) лежит на  оси Оу, следовательно,

x₀=0

Значит, уравнение окружности можно записать так:

(6-0)²+(0-y₀)²=R²  

36+y₀²=R²

или так:

(0-0)²+(8-y₀)²=R²

64-16y+y₀²=R²

Т.к. это два уравнения одной и той же окружности, приравняем их левые части, получим:

36+y₀²=64-16y₀+y₀²

16y₀=64-36

16y₀=28

y₀=1,75

(0;1,75) - координаты центра окружности

Найдём квадрат радиуса окружности:

R²=(8-y₀)²

R²=(8-1,75)²

R²=6,25²

Теперь запишем уравнение  окружности:

(х-0)²+(y-1,75)²=6,25²

x²+(y-1,75)²=30,0625

Объяснение:

Можно лучший? Я хочу умного

Bogdan300707
Bogdan300707
4,6(73 оценок)

14

Объяснение:

По условию треугольник прямоугольный, так как один из его углов прямой. Значит от нас требуется найти гипотенузу AB этого треугольника, зная тангенс одного из углов и прилежащий катет. Тангенс в прямоугольном треугольнике равен отношению противолежащего и прилежащего катетов. То есть:

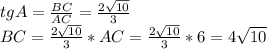
tg A=\frac{BC}{AC}=\frac{2\sqrt{10} }{3} \\BC=\frac{2\sqrt{10} }{3} *AC=\frac{2\sqrt{10} }{3}*6=4\sqrt{10}

Зная катеты можно найти гипотенузу по теореме Пифагора:

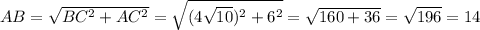
AB=\sqrt{ BC^{2} +AC^{2} }=\sqrt{ (4\sqrt{10}) ^{2} +6^{2} }=\sqrt{160+36}=\sqrt{196}=14

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS