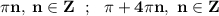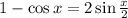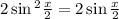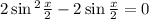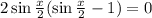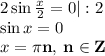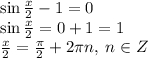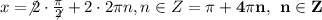Замените a, b, c, d, e, f на числа так, чтобы получилась верная цепочка сравнений 9^123≡a^123≡−b^123≡−(b^5)24⋅b^c≡−d^24⋅e≡f (mod 11). В качестве ответа выберите значения
a =(-5,-2,-1,1,2,5)
b =(-5,-2,-1,1,2,5)
f=(0,1,2,3,4,5,6,7,8,9,10)
133
332
Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Выполните умножение двучленов (0,8c+8d)(6d-0,8c+2d)...
 hjhytu15.10.2022 00:53
hjhytu15.10.2022 00:53 -
Банковский вклад в мае увеличился на 15%, а в июне уменьшился на 10%, после...
 sofijamikisko06.10.2021 14:39
sofijamikisko06.10.2021 14:39 -
Докажите тождество 4(2x-y)^2=(4x-2y)^2...
 danatabilov30.10.2021 05:29
danatabilov30.10.2021 05:29 -
Скількома способами можга утворити тризначні числа з цифр 0,1,5?...
 dsokolovskiyp015em19.12.2022 13:13
dsokolovskiyp015em19.12.2022 13:13 -
Вычислить интеграл, используя формулу интегрирования по частям (подробно):...
 diasline23.01.2022 12:34
diasline23.01.2022 12:34 -
Запишите первые пять членов арифметической прогрессии , если a =4 , d =...
 stepabogocev3724.12.2022 00:16
stepabogocev3724.12.2022 00:16 -
Решите уравнения а) (3x+1)(1-3x)+6x(1,5x+2)=19 б) (7x-5)(7x+5)-24x²=0 в)...
 IdzSen06.01.2020 03:46
IdzSen06.01.2020 03:46 -
Среднее арифметическое трёх чисел — 20. найди эти числа, если первое число...
 ирввадрпраз03.01.2020 05:23
ирввадрпраз03.01.2020 05:23 -
Докажите, что выражение x²-4x+9при любых значениях xпринимает положительные...
 Hi1234901.01.2022 16:56
Hi1234901.01.2022 16:56 -
Чтобы сварить кофе правильно нужно соблюдать пропорции одна третья молока...
 милана0505121.05.2020 18:13
милана0505121.05.2020 18:13

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.