Регистрация Спросить otvet5GPT
egorbokof
06.07.2022 12:41
Математика
Есть ответ 👍

найти наибольшее значение функции на промежутке от [-35;-3] y=(x^+784)/х

122
131
Посмотреть ответы 1

Ответы на вопрос:

ДимаПохитун
ДимаПохитун
4,4(82 оценок)

Применяем формулы сокращённого умножения

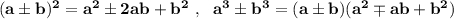\bf (a\pm b)^2=a^2\pm 2ab+b^2\ ,\ \ a^3\pm b^3=(a\pm b)(a^2\mp ab+b^2)   ,

В числителе и знаменателе второй дроби группируем слагаемые и выносим общие множители .

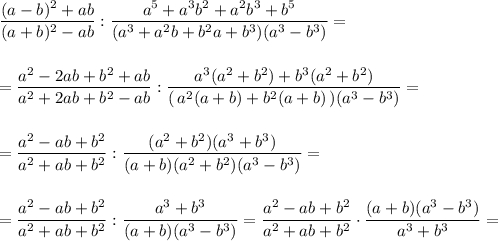
\displaystyle \frac{(a-b)^2+ab}{(a+b)^2-ab}:\frac{a^5+a^3b^2+a^2b^3+b^5}{(a^3+a^2b+b^2a+b^3)(a^3-b^3)}==\frac{a^2-2ab+b^2+ab}{a^2+2ab+b^2-ab}:\frac{a^3(a^2+b^2)+b^3(a^2+b^2)}{(\, a^2(a+b)+b^2(a+b)\, )(a^3-b^3)}==\frac{a^2-ab+b^2}{a^2+ab+b^2}:\frac{(a^2+b^2)(a^3+b^3)}{(a+b)(a^2+b^2)(a^3-b^3)}==\frac{a^2-ab+b^2}{a^2+ab+b^2}:\frac{a^3+b^3}{(a+b)(a^3-b^3)}=\frac{a^2-ab+b^2}{a^2+ab+b^2}\cdot \frac{(a+b)(a^3-b^3)}{a^3+b^3}=

=\dfrac{(a^2-ab+b^2)(a+b)\cdot (a-b)(a^2+ab+b^2)}{(a^2+ab+b^2)\cdot (a+b)(a^2-ab+b^2)}=a-b  

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS