Регистрация Спросить otvet5GPT
nikolay946
28.06.2021 15:48
Алгебра
Есть ответ 👍

Найдите степень и выпишите набор всех коэффициентов многочлена f(x) Найдите степень и выпишите набор всех коэффициентов многочлена f(x)
f(x)=x^6-x^4-x^3
f(x)=x^5-3x^2-7x^3+√3

255
377
Посмотреть ответы 1

Ответы на вопрос:

Maksim9999v
Maksim9999v
4,6(70 оценок)

2\pi - 1

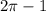
Объяснение:

Подыинтегральная функция на указанном промежутке интегрирования имеет единственную особенность в точке 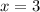x=3. Исследовать интеграл на сходимость в этой точке можно с признака сравнения. В окрестности данной точки данный интеграл эквивалентен интегралу:

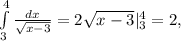
\int\limits_{3}^{4} \frac{dx}{\sqrt{x-3}} = 2\sqrt{x-3}|^{4}_{3} = 2,

то есть исходный интеграл сходится на заданном промежутке. Найдем его:

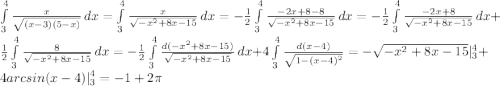
\int\limits_{3}^{4} \frac{x}{\sqrt{(x-3)(5-x)}}\,dx = \int\limits_{3}^{4} \frac{x}{\sqrt{-x^2+8x-15}}\,dx = -\frac{1}{2}\int\limits_{3}^{4} \frac{-2x+8-8}{\sqrt{-x^2+8x-15}}\,dx = -\frac{1}{2}\int\limits_{3}^{4} \frac{-2x+8}{\sqrt{-x^2+8x-15}}\,dx + \frac{1}{2}\int\limits_{3}^{4} \frac{8}{\sqrt{-x^2+8x-15}}\,dx = -\frac{1}{2}\int\limits_{3}^{4} \frac{d(-x^2+8x-15)}{\sqrt{-x^2+8x-15}}\,dx+ 4\int\limits_{3}^{4} \frac{d(x-4)}{\sqrt{1-(x-4)^2}} = -\sqrt{-x^2+8x-15}|^{4}_{3} + 4arcsin(x-4)|^{4}_{3} = -1+2\pi

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS