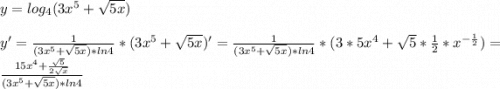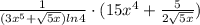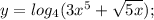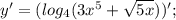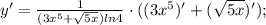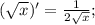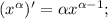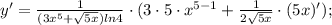Регистрация Спросить otvet5GPT
Бокс111
01.09.2022 06:56
Математика
Есть ответ 👍

Найти производную сложной функции

148
439
Посмотреть ответы 3

Ответы на вопрос:

ЯковНосков
ЯковНосков
4,6(56 оценок)

Пошаговое объяснение:

y=log_4(3x^5+\sqrt{5x})\\\\y'=\frac{1}{(3x^5+\sqrt{5x})*ln4 } *(3x^5+\sqrt{5x} )'=\frac{1}{(3x^5+\sqrt{5x})*ln4 }*(3*5x^4+\sqrt{5}*\frac{1}{2}*x ^{-\frac{1}{2} })=\frac{15x^4+\frac{\sqrt{5} }{2\sqrt{x} } }{(3x^5+\sqrt{5x})*ln4 }

NoraDun
NoraDun
4,7(21 оценок)

\frac{1}{(3x^{5}+\sqrt{5x})ln4} \cdot (15x^{4}+\frac{5}{2\sqrt{5x}})

Пошаговое объяснение:

y=log_{4}(3x^{5}+\sqrt{5x});

y'=(log_{4}(3x^{5}+\sqrt{5x}))';

(f(g(x)))'=f'(g(x)) \cdot g'(x);

(log_{a}x)'=\frac{1}{xlna};

y'=\frac{1}{(3x^{5}+\sqrt{5x})ln4} \cdot (3x^{5}+\sqrt{5x})';

(u \pm v)'=u' \pm v';

y'=\frac{1}{(3x^{5}+\sqrt{5x})ln4} \cdot ((3x^{5})'+(\sqrt{5x})');

(\sqrt{x})'=\frac{1}{2\sqrt{x}};

(x^{\alpha})'=\alpha x^{\alpha-1};

y'=\frac{1}{(3x^{5}+\sqrt{5x})ln4} \cdot (3 \cdot 5 \cdot x^{5-1}+\frac{1}{2\sqrt{5x}} \cdot (5x)');

y'=\frac{1}{(3x^{5}+\sqrt{5x})ln4} \cdot (15x^{4}+\frac{5}{2\sqrt{5x}});

sfsv4641de2r
sfsv4641de2r
4,7(98 оценок)

ответ: r = 15

Пошаговое объяснение:

3/3 = 15/r

находим ОДЗ:

r = 0

3/3 + 15/r,  r ≠ 0

1 = 15/r

r = 15, r ≠ 0

r = 15

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS