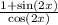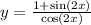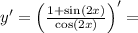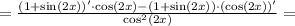Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
решить дам лучший ответ и ...
 ilia20057517.02.2020 21:38
ilia20057517.02.2020 21:38 -
Эки бутун удаалаш сандардын суммасы алардын кобойтундусунон 5 ке кичине.Бул...
 Kastrulya111.10.2021 15:12
Kastrulya111.10.2021 15:12 -
Используя формулу, заполни данную таблицу. y=1,7+x x −6,3 −0,1 3,1 5,2 11,4...
 Denisigroman03.06.2022 22:21
Denisigroman03.06.2022 22:21 -
Решите системы с уравнениями второй степени...
 evakozyreva0315.03.2020 02:38
evakozyreva0315.03.2020 02:38 -
Переведите следующие суждения на язык логики суждений и с таблиц истинности...
 Vika2004040612.08.2020 16:21
Vika2004040612.08.2020 16:21 -
Восстановите порядок действий при решении задачи. Установление зависимости...
 ANNA04050615.04.2020 16:18
ANNA04050615.04.2020 16:18 -
3. Решить уравнение (x-6)=x+12...
 whitreek422311.11.2021 00:43
whitreek422311.11.2021 00:43 -
2) Составьте сюжетную задачу, решение которой приводит к уравнению: олом....
 tat32105.06.2023 17:20
tat32105.06.2023 17:20 -
ставлю 13 балов завдання на фото...
 СпудиМэн14.10.2020 03:38
СпудиМэн14.10.2020 03:38 -
1. Вычислите √2^4×3^2 (число все под корнем) А) 8 Б) 12 Г) 144 B) 24 ...
 khana329.03.2023 20:31
khana329.03.2023 20:31

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.