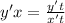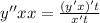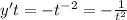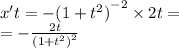Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Масса космического корабля Буран 10 500 000 кг. В стандартном виде...
 TheLaikerMap03.07.2021 13:31
TheLaikerMap03.07.2021 13:31 -
0Используя данные чертежа, узнайте, какой из трех отрезков AB, CD...
 isakdzhanova21.07.2020 23:10
isakdzhanova21.07.2020 23:10 -
Алгебра бжб көмек керек...
 глеб38002.06.2022 11:19
глеб38002.06.2022 11:19 -
file:///C:/Users/%D0%90%D0%BB%D0%B8%D1%88%D0%B0%D0%BD/Desktop/%D0%90%D1%85%D0%BC%D0%B5%D1%82/%D0%90%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0%209%20%D0%A1%D0%9E%D0%A0-1.docx...
 maja626.10.2021 00:37
maja626.10.2021 00:37 -
Разложить на множители а)3а²-9аб б)х²-25х...
 ttleuberlin02.07.2020 15:15
ttleuberlin02.07.2020 15:15 -
Сократить: y^6-y^8\y^4-y^2 решите ,(*...
 Nastya2606122.06.2021 01:47
Nastya2606122.06.2021 01:47 -
Пусть лена задумала число если это число увеличить в 3 раза а потом...
 gidra228133711.08.2020 05:49
gidra228133711.08.2020 05:49 -
Решить , найдите область определения функции: y=√x2-4x+3 + √5-1/5x...
 Senavn21.03.2020 07:15
Senavn21.03.2020 07:15 -
Извесно что f от (x+2) равно икс квадрат минут 7x. найдите функцию...
 Чай2223.03.2022 14:54
Чай2223.03.2022 14:54 -
Надо. брак в продукции завода вследствие дефекта а составляет 5%,...
 lyudsiya133728.12.2022 17:50
lyudsiya133728.12.2022 17:50

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.