Регистрация Спросить otvet5GPT
racinskaulana
17.03.2023 01:25
Алгебра
Есть ответ 👍

Сумма вклада в сберегательный банк увеличивается каждый год на p%. Доказать,что,вложив в банк а рублей через 3 года вкладчик будет иметь на счету а*(1+p/100)^3 рублей можете с объяснением

179
456
Посмотреть ответы 3

Ответы на вопрос:

esenjel
esenjel
4,7(88 оценок)

Объяснение:

Сумма вклада в сберегательный банк увеличивается каждый год на р%. Доказать, что, вложив в банк а рублей, через три года вкладчик будет иметь на счету а •(1+p/100)3nрублей

1234567891248
1234567891248
4,7(70 оценок)

Вкладчик положил в банк "а" рублей под р% годовых.

Через 1 год вкладчик будет иметь на счету  "а" рублей плюс  р%  от "а" рублей.

1% - это 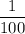  \dfrac{1}{100}   часть числа .

Тогда  р%  -  это 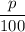  \dfrac{p}{100}   частей от числа "а" равно  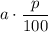a\cdot \dfrac{p}{100}  рублей .

Значит, через 1 год  вкладчик будет иметь на счету

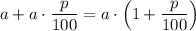  a+a\cdot \dfrac{p}{100}=a\cdot \Big(1+\dfrac{p}{100}\Big)   рублей .

Теперь на счету у вкладчика лежит 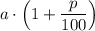  a\cdot \Big(1+\dfrac{p}{100}\Big)  рублей. И теперь на эту сумму в конце 2 года начислят р%, то есть начислят

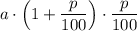  a\cdot \Big(1+\dfrac{p}{100}\Big)\cdot \dfrac{p}{100}   рублей .

Значит, через 2 года на счету вкладчика будет лежать

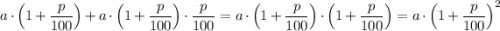  a\cdot \Big(1+\dfrac{p}{100}\Big)+a\cdot \Big(1+\dfrac{p}{100}\Big)\cdot \dfrac{p}{100}=a\cdot \Big(1+\dfrac{p}{100}\Big)\cdot \Big(1+\dfrac{p}{100}\Big)=a\cdot \Big(1+\dfrac{p}{100}\Big)^2  .

Аналогично, через 3 года на счету вкладчика будет лежать

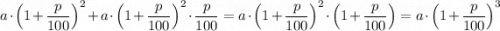
  a\cdot \Big(1+\dfrac{p}{100}\Big)^2+a\cdot \Big(1+\dfrac{p}{100}\Big)^2\cdot \dfrac{p}{100}=a\cdot \Big(1+\dfrac{p}{100}\Big)^2\cdot \Big(1+\dfrac{p}{100}\Big)=a\cdot \Big(1+\dfrac{p}{100}\Big)^3

nikaknekto
nikaknekto
4,7(64 оценок)
Держи ................
Решите уравнение tgx= +‐√3/3

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS