Ксюша0071111

17.12.2021 22:14

Геометрия

Есть ответ 👍

Чи існує трикутник зі сторонами 3 см, 4 см і 8 см?

265

361

Посмотреть ответы 3

Ответы на вопрос:

fiyyk

Геометрия

4,6(24 оценок)

ответ: да

Объяснение: так как он может быть не равносторонний/равнобедренный

arman83

Геометрия

4,7(92 оценок)

Треугольник со сторонам 3 см,4 см и 8 см не существует.

Потому что сумма двух любых сторон треугольника должна быть больше третьей стороны,но в данном случае это не так.

3 + 4 = 7

7 не больше 8

Соответственно такого треугольника не существует.

dok12369

Геометрия

4,5(43 оценок)

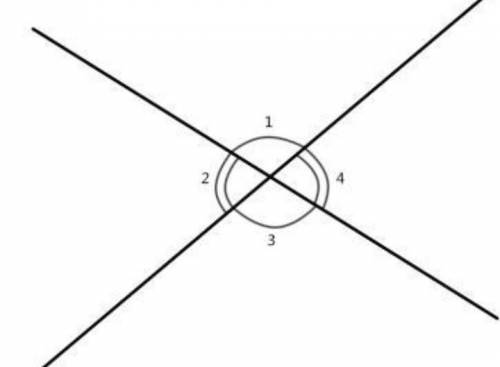
∠1 и ∠3 ; ∠2 и ∠4 - являются вертикальными (по определению).

Естественно, что ∠1 - ∠3 ≠ 37° и ∠2 - ∠4 ≠ 37°, так как по свойству вертикальных углов они равны, (это значит, если вычитать из вертикального угла вертикальный этому углу угол, то получиться 0°).

То есть делаем вывод, что в условии имеется ввиду разность смежных углов.

∠1 и ∠2 - смежные (∠1 > ∠2).

Поэтому, по выше сказанному, пусть ∠1 - ∠2 = 37°.

Смежные углы в сумме дают 180°.

Составим систему и решим её (решим с сложения) :

\{ {\angle 1 + \angle 2 = 180^{\circ} } \atop {\angle 1 - \angle 2 = 37^{\circ}}} .

Складываем обе части уравнений и приводим подобные слагаемые :

∠1 + ∠2 + ∠1 - ∠2 = 180° + 37°

2∠1 = 217° ⇒ ∠1 = 217° : 2 = 108,5°.

Вернёмся во второе уравнение системы, подставим туда значение ∠1 и найдём значение ∠2 :

∠1 - ∠2 = 37°

108,5° - ∠2 = 37°

-∠2 = 37° - 108,5°

-∠2 = -71,5° ⇒ ∠2 = 71,5°.

По выше сказанному :

∠1 = ∠3 = 108,5°

∠2 = ∠4 = 71,5°.

108,5°, 71,5°, 108,5°, 71,5°.

Найдите углы образованные при пересечении двух прямых если один из них равен 37 градусов

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.