Диагональ прямоугольника равна 13 см, а одна из его сторон равна 5 см. Найдите вторую сторону этого треугольника. (Единицу измерения в ответе не указывать).
113
223
Ответы на вопрос:
Отрезок ЕС равен 1 см.
Объяснение:
Требуется найти отрезок ОС.
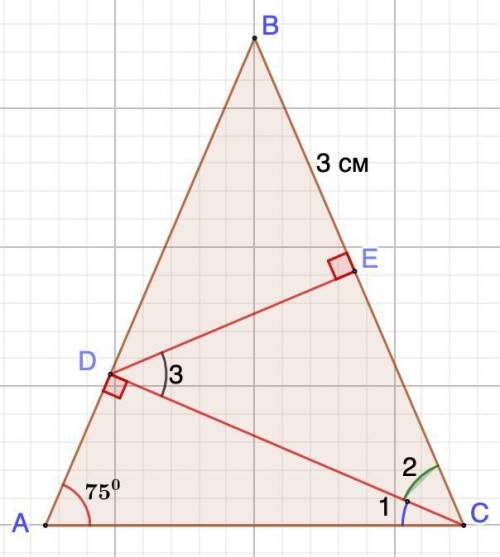
Дано: ΔАВС - равнобедренный;
∠А = 75°;
CD ⊥ АВ; DE ⊥ BC;
ВЕ = 3 см.
Найти: ЕС.
1. Рассмотрим ΔΔАВС - равнобедренный;
Углы при основании равнобедренного треугольника равны.⇒ ∠А = ∠С = 75°
Сумма углов треугольника равна 180°.⇒ ∠В = 180° - (75° + 75°) = 30°
2. Рассмотрим ΔDBE - прямоугольный.
∠В = 30°
Катет, лежащий против угла в 30°, равен половине гипотенузы.Пусть DE = x см, тогда DB = 2x см.
По теореме Пифагора:
BD² = DE² + BE²
4x² = x² + 9
3x² = 9
x² = 3
x = √3
DE = √3 см
3. Рассмотрим ΔАDC - прямоугольный.
Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠1 = 90° - ∠А = 90° - 75° = 15°
4. Рассмотрим ΔEDC - прямоугольный.
∠2 = ∠С - ∠1 = 75° - 15° = 60°
∠3 = 90° - ∠2 = 90° - 60° = 30°
Пусть ЕС = у см, тогда DC = 2у см (катет, лежащий против угла 30°)
По теореме Пифагора:
DC² = DE² + EC²
4y² = 3 + y²
3y² = 3
y² = 1
y = 1
Отрезок ЕС равен 1 см.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Геометрия
-
На стороне ас треугольника авс отметили точку d такую, что ∠abd = ∠c. ав =20см.,...
 ilonka2004801.11.2020 17:34
ilonka2004801.11.2020 17:34 -
Сдиагонали прямоугольника пересекаются в точке о, угол abo=40 градусов.найти...
 gc1220.08.2020 20:42
gc1220.08.2020 20:42 -
Знайти суму кутів тринадцятикутника...
 elkenakate122109.09.2022 17:51
elkenakate122109.09.2022 17:51 -
Help me pls! Определи координаты вершин и сторон треугольника M1N1K1, полученного...
 Licik1625.12.2022 22:32
Licik1625.12.2022 22:32 -
Радиус окружности 12 см, от круга отсечен сектор, градусная мера которого равна...
 yulia626305.04.2023 21:00
yulia626305.04.2023 21:00 -
Треугольник имеет вершины А(8;12), В(-8;0), С(-2;-8). Найдите длину медианы СМ...
 anna5453p08o2210.08.2022 08:56
anna5453p08o2210.08.2022 08:56 -
1). Призма – это выпуклый многогранник, который состоит из: а) многоугольника...
 tanyushalyubim17.12.2021 17:50
tanyushalyubim17.12.2021 17:50 -
Основанием прямой призмы является прямоугольник со сторонами 5дм и 4дм. Боковое...
 katyadk200408.05.2022 18:49
katyadk200408.05.2022 18:49 -
отрезки АВ и CD пересекаются в точке О и точкой пересечения делятся пополам....
 aliolga14.04.2021 20:07
aliolga14.04.2021 20:07 -
Выполнить построение в тетради с кратким пояснением двух задач на построение(построение...
 nikitos13372825.08.2020 09:09
nikitos13372825.08.2020 09:09

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

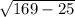 =12
=12