IIIayni

18.12.2021 12:52

Есть ответ 👍

Один вариант выбрать и всё изи Преобразуйте уравнение к виду укажите старший коэффициент, второй коэффициент и свободный член.
А) старший коэффициент 16, второй коэффициент -12 и свободный член -1
В) старший коэффициент -16, второй коэффициент -12 и свободный член 0
С) старший коэффициент 0, второй коэффициент -12 и свободный член 16
D) старший коэффициент -1, второй коэффициент -12 и свободный член 16
E) старший коэффициент 1, второй коэффициент 16 и свободный член -12

279

392

Посмотреть ответы 3

Ответы на вопрос:

vinnnner

Алгебра

4,5(38 оценок)

Объяснение:

(х-4)^2=2х(х+2)

Х^2-2*х*4+4^2=2х^2+4х

Х^2-8х+16-2х^2-4х=0

-х^2-12х+16=0

D) cтарший коффициет - 1

Второй коэффициент - 12

Свободный член 16

maхimus

Алгебра

4,6(72 оценок)

Объяснение:

(x-4)² = 2x(x+2)

x²-8x+16 = 2x² + 4x

-x² - 12x + 16 = 0

nataliolejic

Алгебра

4,7(36 оценок)

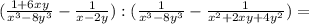
$(\frac{1+6xy}{x^{3}-8y^{3} } - \frac{1}{x-2y} ) : ( \frac{1}{x^{3}-8y^{3}} - \frac{1}{x^{2}+2xy+4y^{2} } ) =$

______________________________

Для справки:

Формула сокращённого умножения

x³-y³ = (x-y)(x²+xy+y²)

______________________________

$= (\frac{1+6xy}{(x-2y)(x^{2} +2xy+4y^{2}) } - \frac{1}{x-2y} ) : ( \frac{1}{(x-2y)(x^{2} +2xy+4y^{2}) } - \frac{1}{x^{2}+2xy+4y^{2} } ) =$

$= \frac{1+6xy -(x^{2} +2xy+4y^{2})}{(x-2y)(x^{2} +2xy+4y^{2}) } : \frac{1-(x-2y)}{(x-2y)(x^{2} +2xy+4y^{2}) } =$

$= \frac{1+6xy -x^{2} -2xy-4y^{2}}{(x-2y)(x^{2} +2xy+4y^{2}) } * \frac{(x-2y)(x^{2} +2xy+4y^{2}) }{1-x+2y} = \frac{-x^{2}+4xy-4y^{2}+1 }{1-x+2y} = -\frac{x^{2}-4xy+4y^{2}-1 }{1-x+2y} =$

$= \frac{(x-2y)^{2}-1 }{1-(x-2y)}$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.