Регистрация Спросить otvet5GPT
Мафаняяя
16.04.2022 04:49
Математика
Есть ответ 👍

уравнение второго порядка привести к каноническому виду, определить тип и основные параметры : 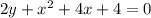2y+x^{2} +4x+4=0

269
303
Посмотреть ответы 1

Ответы на вопрос:

joker249
joker249
4,8(31 оценок)

докажем это с метода индукции. пусть чисел будет не 5, а n.  база при n = 1 утверждение очевидно. действительно, число 200 никак не может оканчиваться на 2009.переход пусть утверждение уже доказано для n = k. покажем, как тогда доказать его для n = k + 2, если k > = 1. по принципу дирихле, так как кольцо вычетов по модулю 2 содержит всего 2 элемента, два из чисел дадут одинаковый остаток при делении на 2. как известно, сумма этих чисел пренепременно окажется четной. не менее широко известно, что разность двух четных чисел четна. понятно, что утверждение можно с числа 200 обобщить до любого четного числа, ведь число 2009 нечетно, а четное число не может быть равно нечетному. обобщим утверждение еще сильнее. если сумма n чисел четна, то их произведение не может быть нечетно. в таком случае переход становится очевиден из того, что, как нетрудно убедиться, произведение четного и любого чисел четно.итак, утверждение верно для n = 1, значит оно верно для n = 3, откуда немедленно следует его справедливость для n = 5, а именно это и требовалось доказать. 

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS