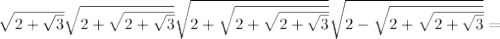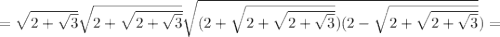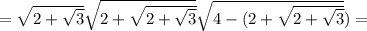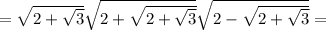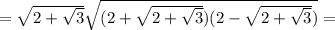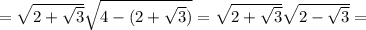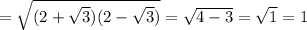Точка пересечения — серединная точка для обоих отрезков и .
Найди величину сторон и в треугольнике , если = 25,9 см и
= 35,2 см
(При ответе упорядочи вершины таким образом, чтобы углы при них были попарно равны.)

NV1.png

А. Так как отрезки делятся пополам, то

1. сторона в треугольнике равна стороне в треугольнике ;

2. сторона в треугольнике равна стороне в треугольнике .

Угoл равен углу как вертикальный угол.

Треугольники равны по первому признаку равенства треугольников.
В равных треугольниках соответствующие стороны равны.

108

293

Посмотреть ответы 1

Ответы на вопрос:

aasssddddddd

Геометрия

4,6(3 оценок)

Объяснение:

$\sqrt{2+\sqrt3}}\sqrt{2+\sqrt{2+\sqrt3}}}\sqrt{2+\sqrt{2+\sqrt{2+\sqrt3}}}}\sqrt{2-\sqrt{2+\sqrt{2+\sqrt3}}}}=\\$

$=\sqrt{2+\sqrt3}}\sqrt{2+\sqrt{2+\sqrt3}}}\sqrt{{(2+\sqrt{2+\sqrt{2+\sqrt3}}})(2-\sqrt{2+\sqrt{2+\sqrt3}}})}=\\$

$=\sqrt{2+\sqrt3}\sqrt{2+\sqrt{2+\sqrt3}}\sqrt{4-(2+\sqrt{2+\sqrt3}})=\\$

$=\sqrt{2+\sqrt3}\sqrt{2+\sqrt{2+\sqrt3}}\sqrt{2-\sqrt{2+\sqrt3}}=\\$ $=\sqrt{2+\sqrt3}\sqrt{(2+\sqrt{2+\sqrt3})(2-\sqrt{2+\sqrt3})}=\\$

$=\sqrt{2+\sqrt3}}\sqrt{4-(2+\sqrt3)}}=\sqrt{2+\sqrt3}}\sqrt{2-\sqrt3}=$

$=\sqrt{(2+\sqrt3)(2-\sqrt3)}=\sqrt{4-3}=\sqrt{1}=1$

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.