Геометрия: ВСЕ признаки равнобедренной трапеции б!

Nikidiy

15.04.2021 01:46

Есть ответ 👍

ВСЕ признаки равнобедренной трапеции б!

175

384

Посмотреть ответы 3

DashaPol09

Геометрия

4,4(48 оценок)

Вот

Объяснение:

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

4.Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

5.Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

kristimisti1234

Геометрия

4,8(2 оценок)

У равнобедренной трапеции углы при основе ровные

У равнобедренной трапеции диагонали равны

lilia25021

Геометрия

4,7(91 оценок)

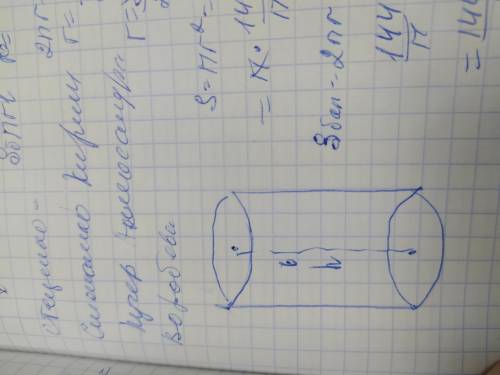
ответ: Sосн=144/π(м²); Sбок.пов=144м²;

Sпол≈189,86м²

Объяснение: площадь боковой поверхности цилиндра вычисляется по формуле: S=2πr×h, где 2πr- длина окружности основания, а h- высота цилиндра:

Sбок.пов=24×6=144м²

Найдём радиус окружности, используя формулу длины окружности: I=2πr

2πr=24

r=24/2π

r=12/π

Теперь найдём площадь основания по формуле: Sосн=πr²

Sосн=π×(12/π)²=π×144/π²=144/π(м²)

Sосн=144/π(м²)

Sпол=Sосн+Sбок.пов=144/π+144=

=(144+144π)/π=(144+144×3,14)/3,14=

=(144+452,16)/3,14=596,16/3,14≈189,86м²

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.