Регистрация Спросить otvet5GPT
regroom
17.04.2021 04:52
Алгебра
Есть ответ 👍

Решите систему неравенств:

186
194
Посмотреть ответы 2

Ответы на вопрос:

rasgramorysergio5775
rasgramorysergio5775
4,4(27 оценок)

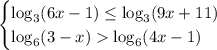
\begin{equation*}\begin{cases}\log_{3}(6x-1) \leq \log_{3}(9x+11)\\\log_{6}(3-x) \log_{6}(4x-1)\end{cases}\end{equation*}

Для начала найдём область допустимых значений переменной x, учитывая все накладываемые на неё ограничения.

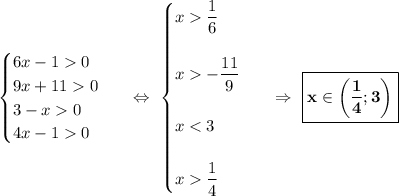
\begin{equation*}\begin{cases}6x - 1 0\\9x + 11 0\\3 - x 0\\4x - 1 0\end{cases}\end{equation*}\ \ \ \Leftrightarrow\ \begin{equation*}\begin{cases}x \dfrac{1}{6}\\\\x -\dfrac{11}{9}\\\\x < 3\\\\x \dfrac{1}{4}\end{cases}\end{equation*}\ \ \ \Rightarrow\ \boxed{\bf{x\in \left(\dfrac{1}{4}; 3\right)}}

Продолжаем решать систему неравенств, но добавляем в неё наше новое ограничение.

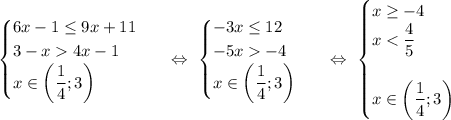
\begin{equation*}\begin{cases}6x - 1 \leq 9x + 11\\3 - x 4x - 1\\x \in \left(\dfrac{1}{4}; 3\right)\end{cases}\end{equation*}\ \ \ \Leftrightarrow\ \begin{equation*}\begin{cases}-3x\leq 12\\-5x -4\\x \in \left(\dfrac{1}{4}; 3\right)\end{cases}\end{equation*}\ \ \ \Leftrightarrow\ \begin{equation*}\begin{cases}x \geq -4\\x < \dfrac{4}{5}\\\\x \in \left(\dfrac{1}{4}; 3\right)\end{cases}\end{equation*}

Откуда получаем, что:

\boxed{\bf{x\in \left(\dfrac{1}{4}; \dfrac{4}{5}\right)}}

avisotska
avisotska
4,6(3 оценок)
А) 3^х=9^х-2 9^2х=9^х-2 2х=х-2 х= -2

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS