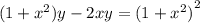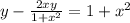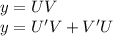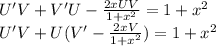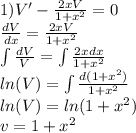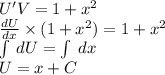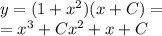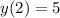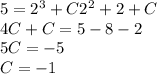Регистрация Спросить otvet5GPT
loooollik
19.12.2021 18:42
Математика
Есть ответ 👍

Решение дифференциального уравнения первого порядка методом Бринелля (1+x^2)y-2xy=(1+x^2)^2 y0=5 x0=2

280
280
Посмотреть ответы 2

Ответы на вопрос:

margaritazaqar
margaritazaqar
4,7(90 оценок)

(1 + {x}^{2} )y - 2xy = {(1 + {x}^{2} )}^{2}

разделим на (1+х^2)

y - \frac{2xy}{1 + {x}^{2} } = 1 + {x}^{2}

это ЛДУ

замена:

y = UV \\ y = U'V + V'U

U'V + V'U - \frac{2xUV}{1 + {x}^{2} } = 1 + {x}^{2} \\ U'V + U(V'- \frac{2xV}{1 + {x}^{2} } ) = 1 + {x}^{2}

1)V' - \frac{2xV}{1 + {x}^{2} } = 0 \\ \frac{dV}{dx} = \frac{2xV}{1 + {x}^{2} } \\ \int\limits \frac{dV}{V} = \int\limits \frac{2xdx}{1 + {x}^{2} } \\ ln(V) = \int\limits \frac{d(1 + {x}^{2}) }{1 + {x}^{2} } \\ ln(V) = ln(1 + {x}^{2} ) \\ v = 1 + {x}^{2}

U'V = 1 + {x}^{2} \\ \frac{dU}{dx} \times (1 + {x}^{2} ) = 1 + {x}^{2} \\ \int\limits \: dU = \int\limits \: dx \\ U = x + C

y = (1 + {x}^{2} )(x + C) = \\ = {x}^{3} + C {x}^{2} + x + C

общее решение

y(2) = 5

5 = {2}^{3} + C {2}^{2} + 2 + C \\ 4C + C = 5 - 8 - 2 \\ 5C = - 5 \\ C= - 1

y = {x}^{3} - {x}^{2} + x - 1

частное решение

Guletta
Guletta
4,4(92 оценок)

Система состоит из трех уравнений.

Из третьего уравнения найдем х-у=-24 => х=у-24

Подставим значение Х в первое уравнение:

2(у-24) - 3у + z = -1

2у-48-3у+z=-1

-y-48+z=-1

z-y=47

Подставим значение Х во второе уравнение:

5(у-24)+2у-z=0

5y-120+2y-z=0

7y-z=120

Получим систему вида:

{z-y=47

{7y-z=120

{x=y-24

Сложим первое и второе уравнения:

6y=167 => y = 167/6

Найдем Х:

Х= 167/6 - 24

Х = 23/6

Найдем Z:

Z = 47 + 167/6

Z = 449/6

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS