Ответы на вопрос:
103 - основание.
1 - показатель степени.
Пошаговое объяснение:
Показатель степени - это число, указывающее количество повторений.
Основание степени - это число, которое умножается само на себя.
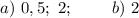
Пошаговое объяснение:
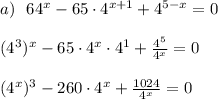
Умножим обе части уравнения на 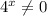 :
:
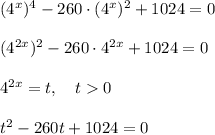
по теореме Виета: 
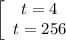
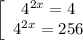
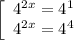
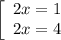
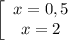
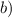 Отберем корни уравнения, принадлежащие отрезку
Отберем корни уравнения, принадлежащие отрезку ![[\log_3{5};\log_3{11}]](/tpl/images/3781/0039/84a2c.png) :
:
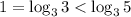 , так как
, так как 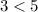 и функция
и функция 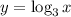 -возрастающая (основание логарифма
-возрастающая (основание логарифма 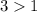 )
)
а 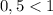 , значит,
, значит, 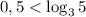 и
и ![0,5 \notin [\log_3{5};\log_3{11}]](/tpl/images/3781/0039/00d12.png)
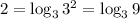 ,
, 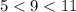 , функция
, функция 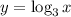 -возрастающая, значит,
-возрастающая, значит, 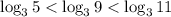 и
и 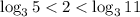 , значит,
, значит, ![2\in [\log_3{5};\log_3{11}]](/tpl/images/3781/0039/eb39e.png)
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Округлите числа 68 823,238 480,2 560 511...
 Madik111111113.11.2022 18:18
Madik111111113.11.2022 18:18 -
Верно ли что при любом значении b значение выражния 6(3-2b)+12b равно 18?...
 darikesa6904.11.2021 10:25
darikesa6904.11.2021 10:25 -
Найдите общий вид первообразной для функции f(x)=1/x^2 -3sin x...
 МИЛ56703.01.2020 22:46
МИЛ56703.01.2020 22:46 -
Правильно решить и записать 4 класса ! а)длина игровой площадки 18м ,а ширина составляет...
 aibekauezhanme07.09.2022 19:05
aibekauezhanme07.09.2022 19:05 -
На одной тарелке 9 пирожков а на другой 7 пирожков даша взяла с этих тарелок 2 пирожка...
 sofia31219.09.2021 15:29
sofia31219.09.2021 15:29 -
Начерти два отрезка так чтобы один был больше другого в 2 раза а вместе они составляли...
 Vlada1209200912.06.2021 01:15
Vlada1209200912.06.2021 01:15 -
Найдите значение выражения 5√0,00032...
 xaverqenizadeoxg0iy13.07.2021 18:50
xaverqenizadeoxg0iy13.07.2021 18:50 -
Смешали 3 сорта конфет: 14 кг по цене 120 р. за 1 кг, 16 кг по 350 р. и 10 кг по...
 omar2809.04.2023 01:01
omar2809.04.2023 01:01 -
Дима построил четырехугольник из карандашей длиной 14 см 10 см 16 см и 8 см костя...
 18Tanya24.02.2020 11:38
18Tanya24.02.2020 11:38 -
Решить за 4 дня бригада озилинителей из 4 рабочих посадила 320 кустов.количество...
 Redimer29.07.2021 07:35
Redimer29.07.2021 07:35

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
