Знайти первісні для функцій/ Найти первоначальные для функций
2.Обчислити/ Вычислить
106
365
Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Моторная лодка прошла 35км по течению и 25км против течения...
 chipssensey29.05.2021 20:54
chipssensey29.05.2021 20:54 -
А)диоганаль прямоугольника равна 17 см а его периметр 46 см...
 karalina20021511.04.2021 22:06
karalina20021511.04.2021 22:06 -
Напишите уравнение прямой, проходящей через точки а (-5; 0)...
 Аркадичка15.11.2022 13:11
Аркадичка15.11.2022 13:11 -
Выполните действия в форме. результат записать в тригонометрической...
 Какэтимпользоваться01.03.2020 02:18
Какэтимпользоваться01.03.2020 02:18 -
Знайдіть екстремум функції f(x)= (...
 Fleepee17.04.2022 22:03
Fleepee17.04.2022 22:03 -
Найти первообразную f(x)=(2x-3)(x^2+4)...
 Викка2315.12.2021 23:35
Викка2315.12.2021 23:35 -
Найдите значение выражения 4,2*10^-2+2,5*10^-1...
 katyushamoshkop0dtz226.11.2021 05:20
katyushamoshkop0dtz226.11.2021 05:20 -
Доопределить функцию f=(1--1-01-), если известно, что она самодвойственная....
 Martinii105.12.2021 08:52
Martinii105.12.2021 08:52 -
Вычислите площадь фигуры ограниченной графиком функции y = (1/2...
 nikitastepanov2119.05.2023 10:49
nikitastepanov2119.05.2023 10:49 -
решить Найдите общий вид первообразной для функции f (х) = cos5x...
 Nastykaramova25.02.2020 22:36
Nastykaramova25.02.2020 22:36

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

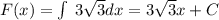
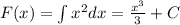
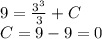
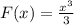
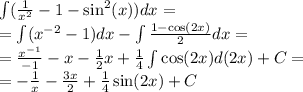
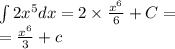
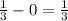
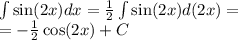
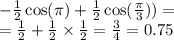
![- 3\int\limits \sqrt[5]{ {x}^{3} } dx = - 3\int\limits {x}^{ \frac{3}{5} } dx = \\ = - 3 \times \frac{ {x}^{ \frac{8}{5} } }{ \frac{8}{5} } + C = - \frac{15}{8} x \sqrt[5]{ {x}^{3} } + C](/tpl/images/4135/4047/23597.png)