Регистрация Спросить otvet5GPT
ytytuty
29.10.2022 19:14
Геометрия
Есть ответ 👍

1)Плоскости α и β параллельны. Прямые a и b принадлежат плоскостям α и β соответственно. Через прямую a проведена плоскость, которая пересекает плоскость β по прямой c, которая параллельна прямой b. Как расположены прямая a и прямая b? 2)Точка O – общая середина каждого из отрезков AA1, BB1, CC1, которые не лежат в одной плоскости. Укажите взаимное расположение плоскостей (ABC) и (A1B1C1).
3)Точки A и B расположены в одной из двух параллельных плоскостях, точки C и D – во второй. Отрезки AC и BD пересекаются в точке M. Как расположены прямые AB и CD?
4)На рисунке изображен куб ABCDA1B1C1D1. Определите параллельные плоскости, которые содержат скрещивающиеся прямые B1C1 и DD1. (Фото сюда)
5)Треугольник AED и параллелограмм ABCD не лежат в одной плоскости. Точки M и K – середины сторон AE и ED соответственно. Найдите MK, если BC=8 см.
6)Прямая a параллельна плоскости α. Через точки A и B прямой a проведены параллельные прямые, которые пересекают плоскость α в точках A1 и B1 соответственно. Найти площадь четырехугольника AA1B1B, если A1B1 =17 см, AB1=10 см, BB1=21 cм.

173
267
Посмотреть ответы 1

Ответы на вопрос:

MINdana
MINdana
4,5(88 оценок)

ответ: 6.6м

Объяснение: Так как периметр треугольника равен сумме его сторон , то имеем что AB+BC+AC=15.2 Если у нас треугольник равнобедренный , то боковые стороны равны друг другу. Составляем уравнение, подставляем значение и так как АС неизвестно , ставим x. Получаем уравнение и решаем

4.3+4.3+x=15.2.

8.6+x=15.2

x=15.2-8.6

x=6.6

Следовательно Основание AC=6.6


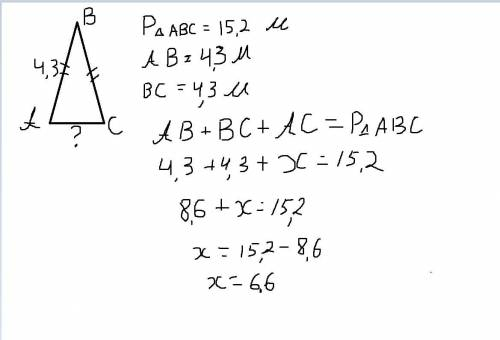
Пириметр равнобедренного треугольника равен 15.2 м а боковой сторона равна 4.3 м найдите основание

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS