Математика: Кіт собака миша зерно мед дракула

Алёна1570

01.08.2021 07:24

Математика

Есть ответ 👍

Кіт собака миша зерно мед дракула

244

261

Посмотреть ответы 1

Ответы на вопрос:

аор8

Математика

4,4(91 оценок)

Пошаговое объяснение:

Номер 1. 90<α<180, cos(α)=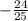 $-\frac{24}{25}$

Ограничения на угол α накладывают ограничения на sin(α): sin(α) >0 , т.к. угол находится во второй четверти.

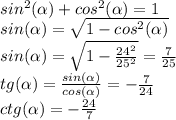
$sin^2(\alpha )+cos^2(\alpha)=1\\sin(\alpha)=\sqrt{1-cos^2(\alpha)}\\ sin(\alpha)=\sqrt{1-\frac{24^2}{25^2} }=\frac{7}{25} \\ tg(\alpha)=\frac{sin(\alpha)}{cos(\alpha)} =-\frac{7}{24}\\ ctg(\alpha)=-\frac{24}{7}$

Номер 2.

а) cos(3π/5)*tg(π/9)

Сравним каждый множитель с 0:

tg(π/9)>0 т.к. sin(π/9)>0 и cos(π/9) >0, и если делить положительное число на положительное, то получится положительное

cos(3π/5) : 3π/5 - тупой угол => его косинус отрицательный

Мы умножаем положительное число на отрицательное и получаем отрицательное => cos(3π/5)*tg(π/9)<0

б)sin(4)cos(5)

Аналогично:

sin(4): π<4<2π=> sin(4)<0

cos(5): 3π/2<5<5π/2 =>cos(5)>0

sin(4)cos(5)<0

Номер 5.

$8sin^2(\alpha )-5cos^2(\alpha)=7\\cos^2(\alpha)=1-sin^2(\alpha)\\8sin^2(\alpha)-5(1-sin^2(\alpha))=7\\8sin^2(\alpha)-5+5sin^2(\alpha)=7\\13sin^2(\alpha)=12\\sin^2(\alpha)=\frac{12}{13}\\ cos^2(\alpha)=\frac{1}{13}\\ tg^2(\alpha)=\frac{sin^2(\alpha)}{cos^2(\alpha)}=12$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.