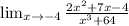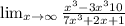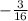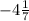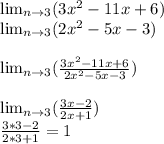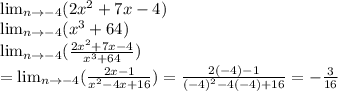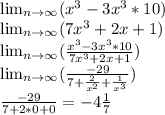Ответы на вопрос:
ответ: 1) 2 1/5
2) 5 1/3
3) 2 1/2 (2,5)
Пошаговое объяснение:
1) х=2+1/5
2)х=1 1/3+4
3)х=2+1/2
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Як довести що числа 35 і 32 взаємно прості...
 skripniklenok1322.02.2020 11:35
skripniklenok1322.02.2020 11:35 -
З двох міст назустріч виїхали 2поїзди. Через 14год вони зустрілися.Швидкість...
 Аноним812717.07.2021 12:05
Аноним812717.07.2021 12:05 -
Решите задание 8 с полным оформлением и решением....
 Alrksanr16.02.2022 17:53
Alrksanr16.02.2022 17:53 -
Скорость катера по течению реки 28 км/ч, а против течения 22км/ч. Найдите...
 F1kser18.06.2020 15:20
F1kser18.06.2020 15:20 -
Возьми сосуд на ливнева воду объём её должен быть равен K соответственно записи...
 Zlowmak17.11.2022 07:35
Zlowmak17.11.2022 07:35 -
На координатной плоскости постройте точки A(-2;4),B(-1;-3),C(1;5);D(1;-3);E(-5;2);K(0;-1)....
 Нови4ок22827.01.2022 23:01
Нови4ок22827.01.2022 23:01 -
Для урока труда купили 3 набора цветной бумаги по 12 листов в каждом и 50...
 AIDA90223109.12.2022 21:16
AIDA90223109.12.2022 21:16 -
Решите уравнения: (х + 1,8) – 6,01 = 10,4....
 alinamensikova02.09.2020 00:51
alinamensikova02.09.2020 00:51 -
Периметр квадрата 22,48 дм. найдите его площадь. ответ округлите до десятых...
 DariaMejor19.03.2020 02:19
DariaMejor19.03.2020 02:19 -
Для уроков труда купили 3 набора цветной бумаги по 12 листов в каждом и 50...
 даша317130.01.2020 17:12
даша317130.01.2020 17:12

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

 2.
2.