характеристика порівняльна таблиця головних героїв повісті альпійська балада,если что зарубежка извиняюсь

129

158

Посмотреть ответы 1

Ответы на вопрос:

antonnetyaga

Немецкий язык

4,4(80 оценок)

наибольшее значение функции равно 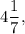$4\dfrac{1}{7} ,$ а наименьшее значение функции равно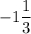 $-1\dfrac{1}{3}$

Объяснение:

Найти наибольшее и наименьшее значение функции

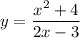$y=\dfrac{x^{2} +4}{2x-3}$ на промежутке [ 0; 5]

Так как делить на нуль нельзя, то 2х -3 ≠0, то есть х ≠ 1,5.

Тогда область определение функции: D(y) = ( -∞ ; 1,5 ) ∪(1,5; + ∞)

Найдем производную функции

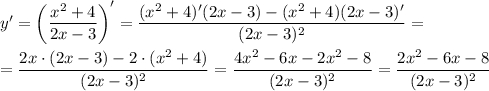
$y'=\left(\dfrac{x^{2} +4}{2x-3}\right)'= \dfrac{(x^{2} +4)'(2x-3) - (x^{2} +4)(2x-3)'}{(2x-3)^{2} } ==\dfrac{2x\cdot(2x-3) -2\cdot( x^{2} +4)}{(2x-3)^{2} } =\dfrac{4x^{2} -6x-2x^{2} -8}{(2x-3)^{2} } =\dfrac{2x^{2} -6x -8}{(2x-3)^{2} }$

Найдем критические точки, решив уравнение: y' = 0.

Дробь равна нулю, если числитель равен нулю

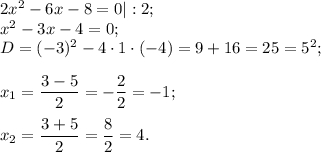
$2x^{2} -6x -8=0|:2;\\x^{2} -3x-4=0;\\D =(-3)^{2} -4\cdot1\cdot (-4)= 9+16=25 =5^{2} ;x{_1}= \dfrac{3-5}{2} =-\dfrac{2}{2} =-1;x{_2}= \dfrac{3+5}{2} =\dfrac{8}{2} =4.$

Заданному промежутку [ 0; 5] принадлежит х =4.

Найдем значение функции на концах промежутка и в точке х =4 .

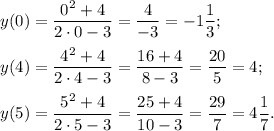
$y(0)=\dfrac{0^{2} +4}{2\cdot 0-3}=\dfrac{4}{-3} =-1\dfrac{1}{3} ;y(4)=\dfrac{4^{2} +4}{2\cdot4-3}=\dfrac{16+4}{8-3} =\dfrac{20}{5} =4;y(5)=\dfrac{5^{2} +4}{2\cdot5 -3}=\dfrac{25+4}{10-3} =\dfrac{29}{7} =4\dfrac{1}{7} .$

Сравним найденные значения и получим, что наибольшее значение функции равно 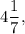$4\dfrac{1}{7} ,$ а наименьшее значение функции равно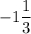 $-1\dfrac{1}{3}$

#SPJ1

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Немецкий язык

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.