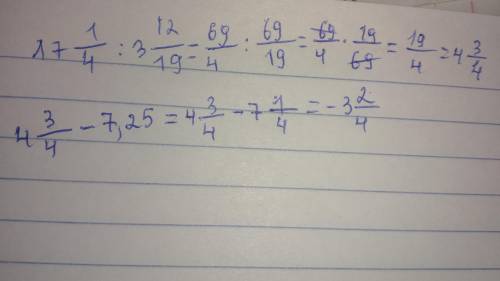Ответы на вопрос:
Выделим квадрат разности в знаменателе:
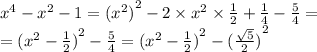
Получаем:
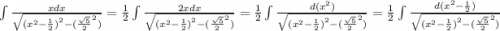
получили табличный интеграл:
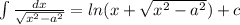
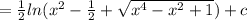
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Написать первые пять членов ряда по заданному общему члену an=1/(2n-1)(2n+1)...
 aleksandrakival298930.03.2021 18:19
aleksandrakival298930.03.2021 18:19 -
Придумайте загадку ответом которой будет лекционный кабинет...
 omsbksrj09.07.2020 17:54
omsbksrj09.07.2020 17:54 -
Допустим, аннабель едет на поезде polar express на северный полюс. длина поезда...
 агроэШкольник228105.07.2020 07:14
агроэШкольник228105.07.2020 07:14 -
Одна целая 1/8 + 3/8 = объясните как решить,заранее ....
 Viktor1510211.10.2021 14:24
Viktor1510211.10.2021 14:24 -
Найдите значение выражения (306 х 307 - 187 х 36): 45 + 5780...
 marchaika201420.07.2020 04:05
marchaika201420.07.2020 04:05 -
Решите . надо! первую часть пути автомобиль ехал со скоростью в два раза больше,...
 Maximg0118.08.2022 09:02
Maximg0118.08.2022 09:02 -
Расстояние на карте между двумя равно 2,5 см . найди масштаб карты если расстояние...
 mashasandalkina09.07.2020 18:58
mashasandalkina09.07.2020 18:58 -
В7 одинаковых коробках 49 карандашей. сколько таких коробок потребуется, чтобы разложить...
 Anastasiagoodnastia03.06.2020 06:43
Anastasiagoodnastia03.06.2020 06:43 -
Аквариум имеет форму прямоугольного параллелепипедов длина которого 45 см ширина...
 Privetcsfvxs25.11.2020 04:13
Privetcsfvxs25.11.2020 04:13 -
Кыш турында дэрэжэлэр белэн кулланып хикэя язырга(дэрэжэлэр- гади,артыклык,чагыштыру...
 vlad01626362452467720.09.2021 13:32
vlad01626362452467720.09.2021 13:32

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.