Геометрия: Виконати завдання на фото № 78, 79, 82, 86, 87

olga7882

04.01.2022 05:29

Геометрия

Есть ответ 👍

Виконати завдання на фото № 78, 79, 82, 86, 87

268

436

Посмотреть ответы 3

Ответы на вопрос:

Maksikar

Геометрия

4,7(5 оценок)

Объяснение:

78. Рассмотрим ∆АВД и ∆СВД.

У них: 1) ВД — общая;

2) угол АДВ = углу СДВ (по условию);

3) АД= СД (по условию);

Значит, ∆АВД=∆СВД (по двум сторонам и углу между ними).

ч.т.д.

79. Рассмотрим ∆АВД и ∆СВД.

У них: 1) ВД - общая.

2) угол АДВ = углу СВД (по условию);

3) АД=ВС (по условию).

Значит, ∆АВД=∆СВД (по двум сторонам и углу между ними).

86. Рассмотрим ∆АВД и ∆СВД.

У них: 1) ВД - общая;

2) угол АВД = углу СВД (по условию);

3) угол ВДА = углу ВДС (по условию);

Значит, ∆АВД=∆СВД (по стороне и прилежащим к ней углам).

87. Рассмотрим ∆АВД и ∆СВД.

У них: 1) ВД - общая;

2) угол АВД= углу СДВ (по условию);

3) угол АДВ = углу СВД (по условию);

Значит, ∆АВД=∆СВД (по стороне и прилежащим к ней углам)

нчшрдтснь

Геометрия

4,5(92 оценок)

78. ΔADB = ΔCDB по двум сторонам (AD = CD, а также общая сторона BD) и углу между ними (∠ADB = ∠CDB), то есть по первому признаку равенства треугольников.

79. ΔADB = ΔCDB по двум сторонам (AD = BC, а также общая сторона BD) и углу между ними (∠ADB = ∠CBD), то есть по первому признаку равенства треугольников.

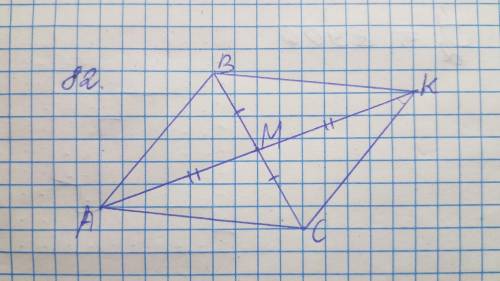
82. ΔACM = ΔKBM по двум сторонам (BM = MC, AM = MK) и углу между ними (∠BMK = ∠AMC, так как эти углы вертикальные), то есть по первому признаку равенства треугольников. Рисунок к задаче на фото.

86. ΔADB = ΔCDB по стороне (общая сторона BD) и двум прилежащим углам (∠ABD = ∠CBD, ∠ADB = ∠CDB), то есть по второму признаку равенства треугольников.

87. ΔADB = ΔCDB по стороне (общая сторона BD) и двум прилежащим углам (∠ABD = ∠CDB, ∠ADB = ∠CBD), то есть по второму признаку равенства треугольников.

Виконати завдання на фото № 78, 79, 82, 86, 87

vikook1

Геометрия

4,7(21 оценок)

155

Объяснение:

AOF=180-(AOB+FOE)

180-(54+25)=101

AOF=COD

AOB=EOD

COE=COD+EOD

COE=101+54

COE=155

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.