Регистрация Спросить otvet5GPT
TsunamiBrain
01.11.2020 19:53
Геометрия
Есть ответ 👍

Номер 2.56
с 1 по 5
с объяснением.​

283
339
Посмотреть ответы 2

Ответы на вопрос:

cfgcgj
cfgcgj
4,5(22 оценок)

В таких заданиях в основном ведётся работа с формулами. Прежде, чем притупить к заданям, вспомним формулу основного тригоносетрического тождества, которая в основном тут и будет использоваться:

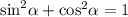
{ \sin }^{2} \alpha + { \cos}^{2} \alpha = 1

1) Если мы воспользуемся основным тригоносетрическим тождеством, выразив оттуда косинус в квадрате, то получим как раз таки это выражение, значит его можно упростить так:

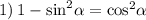
1) \: 1 - { \sin }^{2} \alpha = { \cos}^{2} \alpha

2) Аналогично предыдущему, тоже опираясь на основное тригоносетрическое тождество, получим:

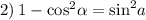
2) \: 1 - { \cos}^{2} \alpha = { \sin }^{2} a

3) Это выражение для начала можно сложить по формуле разности квадратов, после чего преобразуем полученное выражение так же, как и во втором:

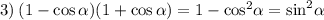
3) \: (1 - \cos\alpha )(1 + \cos \alpha ) = 1 - { \cos }^{2} \alpha = { \sin }^{2} \alpha

4) Опять же, опираясь на основное тригоносетрическое тождество можно синус в квадрате плюс косинус в квадрате заменить на единицу, в результате чего мы получим:

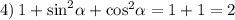
4) \: 1 + { \sin}^{2} \alpha + { \cos}^{2} \alpha = 1 + 1 = 2

5) Вынесем за скобку синус, а полученное выражение преубразуем, опять же, как во втором пункте:

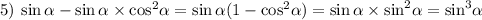
5) \: \sin \alpha - \sin \alpha \times { \cos }^{2} \alpha = \sin \alpha (1 - { \cos }^{2} \alpha ) = \sin \alpha \times { \sin }^{2} \alpha = { \sin }^{3} \alpha

lddld
lddld
4,6(4 оценок)

Площадь круга S = 59,29* дм²

Объяснение:

Углы OEF и ОFE равны. При этом сумма этих углов = 180° - угол EOF = 180° - 60° = 120°. Т.е. все углы треугольника OFE равны 60°. Это признак равностороннего треугольника. Следовательно хорда EF = радиусу окружности R.

Площадь круга S = *R² = *(7,7)²дм² = 59,29* дм²

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS